|
题文
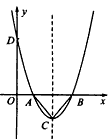
| 一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC。 |
|
|
(1)若m为常数,求抛物线的解析式;
(2)若m为小于O的常数,那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点?
(3)设抛物线交y轴正半轴于D点,问是否存在实数m,使得△BOD为等腰三角形?若存在,求出m的值;若不存在,请说明理由。 |
题型:解答题 难度:偏难
答案
解:(1)设抛物线的解析式为:y=a(x-m+2)(x-m-2)=a(x-m)2-4a,
∵AC⊥BC,由抛物线的对称性可知:△ACB为等腰直角三角形,又AB=4,
∴C(m,-2)代入得a= , ,
∴解析式为:y=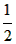 (x-m)2-2; (x-m)2-2;
(2)∵m为小于0的常数,
∴只需将抛物线向右平移-m个单位,再向上平移2个单位,
可以使抛物线y= (x-m)2-2顶点在坐标原点; (x-m)2-2顶点在坐标原点;
(3)由(1)得D(0, m2-2),设存在实数m,使得△BOD为等腰三角形, m2-2),设存在实数m,使得△BOD为等腰三角形,
∵△BOD为直角三角形,
∴只能OD=OB,
∴ m2-2=|m+2|, m2-2=|m+2|,
当m+2>0时,解得m=4或m=-2(舍),
当m+2<0时,解得m=0(舍)或m=-2(舍);
当m+2=0时,即m=-2时,B、O、D三点重合(不合题意,舍),
综上所述:存在实数m=4,使得△BOD为等腰三角形。 |
据专家权威分析,试题“一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线..”主要考查你对 求二次函数的解析式及二次函数的应用,等腰三角形的性质,等腰三角形的判定,平移 等考点的理解。关于这些考点的“档案”如下:
求二次函数的解析式及二次函数的应用等腰三角形的性质,等腰三角形的判定平移
考点名称:求二次函数的解析式及二次函数的应用 考点名称:等腰三角形的性质,等腰三角形的判定 考点名称:平移
|

