|
题文
| 如图,平面直角坐标系中有一直角梯形OMNH,点H的坐标为(-8,0),点N的坐标为(-6,-4)。 |
|

|
(1)画出直角梯形OMNH绕点O旋转180°的图形OABC,并写出顶点A,B,C的坐标(点M的对应点为A,点N的对应点为B,点H的对应点为C);
(2)求出过A,B,C三点的抛物线的表达式;
(3)截取CE=OF=AG=m,且E,F,G分别在线段CO,OA,AB上,求四边形BEFG的面积S与m之间的函数关系式,并写出自变量m的取值范围;面积S是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;
(4)在(3)的情况下,四边形BEFG是否存在邻边相等的情况,若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由。 |
题型:解答题 难度:偏难
答案
解:(1)利用中心对称性质,画出梯形OABC,图“略”;
∵A,B,C三点与M,N,H分别关于点O中心对称,
∴A(0,4),B(6,4),C(8,0);
(2)设过A,B,C三点的抛物线关系式为 , ,
∵抛物线过点A(0,4),
∴c=4,则抛物线关系式为 , ,
将B(6,4),C(8,0)两点坐标代入关系式,得
 ,解得 ,解得 ,所求抛物线关系式为: ,所求抛物线关系式为: ; ;
(3)∵OA=4,OC=8,
∴AF=4-m,OE=8-m,
∴ = = OA(AB+OC)- OA(AB+OC)- AF·AG- AF·AG- OE·OF- OE·OF- CE·OA CE·OA
= = = (0<<4), (0<<4),
∵ , ,
∴当m=4时,S取最小值,
又∵0<m<4,
∴不存在m值,使S取得最小值;
(4)当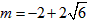 时,GB=GF,当m=2时,BE=BG。 时,GB=GF,当m=2时,BE=BG。 |
 |
据专家权威分析,试题“如图,平面直角坐标系中有一直角梯形OMNH,点H的坐标为(-8,0),..”主要考查你对 求二次函数的解析式及二次函数的应用,二次函数的最大值和最小值,图形旋转 等考点的理解。关于这些考点的“档案”如下:
求二次函数的解析式及二次函数的应用二次函数的最大值和最小值图形旋转
考点名称:求二次函数的解析式及二次函数的应用 考点名称:二次函数的最大值和最小值 考点名称:图形旋转
|

