 |
首页 > 考试 > 数学 > 初中数学 > 条形图 > 正文 | 返回 打印 |
|
|
首页 > 考试 > 数学 > 初中数学 > 条形图 > 正文 | 返回 打印 |
|
答案
（1）补充图形如下： ； （2）360°×40%=144°； （3）A的投票得分是：300×35%=105（分）， 则A的最后得分是：
B的投票得到是：300×40%=120（分）， 则B的最后得分是：
C的投票得分是：300×25%=75（分）， 则C的最终得分是：
所以B当选． |
据专家权威分析，试题“A，B，C三名大学生竞选系学生会主席，他们的笔试成绩和口试成绩（..”主要考查你对 条形图，平均数，统计表 等考点的理解。关于这些考点的“档案”如下：
条形图平均数统计表
考点名称：条形图
条形图特点：
（1）能够显示每组中的具体数据；
（2）易于比较数据之间的差别。
描绘条形图的3要素：组数、组宽度、组限。
1.组数
把数据分成几组，指导性的经验是将数据分成5~10组。
2.组宽度
通常来说，每组的宽度是一致的。组数和组宽度的选择就不是独立决定的，一个经验标准是：
近似组宽度=（最大值-最小值）/组数
然后根据四舍五入确定初步的近似组宽度，之后根据数据的状况进行调整。
3.组限
分为组下限（进入该组的最小可能数据）和组上限（进入该组的最大可能数据），并且一个数据只能在一个组限内。
绘画条形图时，不同组之间是有空隙的；而绘画直方图时，不同组之间是没有空隙的。
使用条形图的情况：
轴标签过长；
显示的数值是持续型的。
条形图具有下列图表子类型：
簇状条形图和三维簇状条形图 簇状条形图比较各个类别的值。在簇状条形图中，通常沿垂直轴组织类别，而沿水平轴组织数值。三维簇状条形图以三维格式显示水平矩形，而不以三维格式显示数据。
堆积条形图和三维堆积条形图 堆积条形图显示单个项目与整体之间的关系。三维堆积条形图以三维格式显示水平矩形，而不以三维格式显示数据。
百分比堆积条形图和三维百分比堆积条形图 此类型的图表比较各个类别的每一数值所占总数值的百分比大小。三维百分比堆积条形图表以三维格式显示水平矩形，而不以三维格式显示数据。
水平圆柱图、圆锥图和棱锥图 水平圆柱图、圆锥图和棱锥图可以使用为矩形条形图提供的簇状图、堆积图和百分比堆积图，并且它们以完全相同的方式显示和比较数据。唯一的区别是这些图表类型显示圆柱、圆锥和棱锥形状而不是水平矩形。
考点名称：平均数
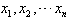，那么 
，叫做这n个数的算术平均数。 
点的权分别为
，那么称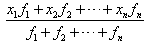
为这n个数的加权平均数。 平均数、中位数和众数关系:
联系:
平均数、中位数和众数都是来刻画数据平均水平的统计量，它们各有特点。对于平均数大家比较熟悉，中位数刻画了一组数据的中等水平，众数刻画了一组数据中出现次数最多的情况。
平均数非常明显的优点之一是，它能够利用所有数据的特征，而且比较好算。另外，在数学上，平均数是使误差平方和达到最小的统计量，也就是说利用平均数代表数据，可以使二次损失最小。因此，平均数在数学中是一个常用的统计量。但是平均数也有不足之处，正是因为它利用了所有数据的信息，平均数容易受极端数据的影响。
例如，在一个单位里，如果经理和副经理工资特别高，就会使得这个单位所有成员工资的平均水平也表现得很高，但事实上，除去经理和副经理之外，剩余所有人的平均工资并不是很高。这时，中位数和众数可能是刻画这个单位所有人员工资平均水平更合理的统计量。
中位数和众数这两个统计量的特点都是能够避免极端数据，但缺点是没有完全利用数据所反映出来的信息。
由于各个统计量有各自的特征，所以需要我们根据实际问题来选择合适的统计量。
当然，出现极端数据不一定用中位数，一般，统计上有一个方法，就要认为这个数据不是来源于这个总体的，因而把这个数据去掉。比如大家熟悉的跳水比赛评分，为什么要去掉一个最高分、一个最低分呢，就认为这两个分不是来源于这个总体，不能代表裁判的鉴赏力。于是去掉以后再求剩下数据的平均数。需要指出的是，我们处理的数据，大部分是对称的数据，数据符合或者近似符合正态分布。这时候，均值(平均数)、中位数和众数是一样的。
区别:
只有在数据分布偏态(不对称)的情况下，才会出现均值、中位数和众数的区别。所以说，如果是正态的话，用哪个统计量都行。如果偏态的情况特别严重的话，可以用中位数。
除了需要刻画平均水平的统计量，统计中还有刻画数据波动情况的统计量。比如，平均数同样是5，它所代表的数据可能是1、3、5、7、9，可能是4、4.5、5、5.5、6。也就是说5所代表的不同组数据的波动情况是不一样的。怎样刻画数据的波动情况呢?很自然的想法就是用最大值减最小值，即求一组数据的极差。数学中还有方差、标准差等许多用来刻画数据特征的统计量。当然这些都是教师感兴趣、值得了解的内容，不是小学数学的教学要求。
； 
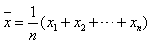。 考点名称：统计表
统计表构成及格式：
一般由表头、行标题、列标题和数字资料四个主要部分组成，必要时可以在统计表的下方加上表外附加。
①表头应放在表的上方，它所说明的是统计表的主要内容。
②行标题和列标题通常安排在统计表的第一列和第一行，它所表示的主要是所研究问题的类别名称和指标名称，通常也被称为“类”。
③表外附加通常放在统计表的下方，主要包括资料来源、指标的注释、必要的说明等内容。
结构：
①总标题――概括统计表中全部资料的内容，是表的名称。
②横行标题――表示各组的名称，它说明统计表要说明的对象，是横行的名称。
③纵栏标题――表示汇总项目即统计指标的名称。
④数字资料――是各组、各汇总项目的数值。列在各横行标题与各纵栏标题交叉处，即统计表的右下方。
内容构成：
主词――是说明总体的，它可以是各个总体单位的名称、总体各个分组名称。行式上表现为横行标题。
宾词――是说明总体的指标名称和数值的。形式上表现为纵栏标题和指标数值。
统计表分类：
统计表形式繁简不一，通常是按项目的多少，分为单式统计表与复式统计表两种。只对某一个项目数据进行统计的表格，称为单式统计表，也称之为简单统计表。统计项目在2个或2个以上的统计表格，称之为复式统计表。
1、按作用不同：统计调查表、汇总表、分析表。
2、按分组情况不同：简单表、简单分组表、复合分组表。
①简单表：即不经任何分组，仅按时间或单位进行简单排列的表。
②简单分组表：即仅按一个标志进行分组的表。
③复合分组表：即按两个或两个以上标志进行层叠分组的表。
统计表设计：
由于使用者的目的以及统计数据的特点不同，统计表的设计在形式和结构上会有较大差异，但设计的基本要求是一致的。总体上来说，统计表的设计应符合科学、实用、简练、美观的要求。具体来说设计统计表时要注意以下几点：
1.合理安排统计表的结构。比如行标题、列标题、数字资料的位置应安排合理。
2.表头一般应包括表号、总标题和表中数据的单位等内容。
总标题应简明确切地概括出统计表的内容，一般需要表明统计数据的时间、地点以及何种数据，即标题内容应满足3W(统计数据的时间、地点、何种数据的简称)要求。
3.如果表中的全部数据都是同一计量单位，可放在表的右上角标明，若各指标的计量单位不同，则应放在每个指标后或单列出一列标明。
4.表中的上下两条线一般用粗线，中间的其他线要用细线，这样使人看起来清楚、醒目。
5.在使用统计表时，必要时可在表的下方加上注释，特别要注明资料来源，以表示对他人劳动成果的尊重，方便读者查阅使用。
统计表制作规则:
1、统计表一般为横长方形，上下两端封闭且为粗线，左右两端开口。
2、统计表栏目多时要编号，一般主词部分按甲、乙、丙；宾词部分按(1)(2)等次序编号。
3、统计表总标题应简明扼要，符合表的内容。
4、主词与宾词位置可互换。各栏排列次序应以时间先后、数量大小、空间位置等自然顺序编排。
5、计量单位一般写在表的右上方或总栏标题下方。
6、表内资料需要说明解释部分，如：注解、资料来源等，写在表的下方。
7、填写数字资料不留空格，即在空格处划上斜线。统计表经审核后，制表人和填报单位应签名并盖章，以示负责。
