|
题文
如图①在正方形网格中有四边形ABCD.
(1)利用网格作∠A、∠B的平分线;
(2)∠A、∠B的平分线交于点O,判断点O是否在其他两个角的平分线上;
(3)从图中你还能发现什么结论?
(4)如图②,在四边形ABCD中四个内角平分线仍相交于一点O,在上面这些结论中,哪些是必然事件,哪些是随机事件?试说明理由。 |
  |
题型:解答题 难度:偏难
答案
(1)“略”
(2)“略”
(3)结论有①AD∥BC;②∠AOB=∠DOC=90°;③AD+BC=AB+CO; ④S△ABC=S△ABO;⑤∠ADD与∠BOC互补
(4)如果满足四个内角平分线相交于一点,则结论③④是必然事件,而结论①②⑤是随机事件。
理由如下:
①若AD∥BC,则∠BAD+∠ABC=180°,因为OA平分∠BAD,所以∠1= ∠BAD, ∠BAD,
同理∠2=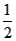 ∠ABC,所以∠1+∠2= ∠ABC,所以∠1+∠2=  (∠BAD+∠ABC)= (∠BAD+∠ABC)=  ×180°=90°,显然不成立。 ×180°=90°,显然不成立。
同样②⑤也不一定成立。
③过点O向四边作垂线,垂足为E、F、G、日,由条件易证AE=AF,DE=DH,BF=BG,CG=CH,
所以,AB+BC=AE+DE+BG+GC=AF+DH+BF+CH=AB+CD |
据专家权威分析,试题“如图①在正方形网格中有四边形ABCD.(1)利用网格作∠A、∠B的平分线;..”主要考查你对 角平分线的定义 ,随机事件,平行线的判定,角平分线的性质 等考点的理解。关于这些考点的“档案”如下:
角平分线的定义 随机事件平行线的判定角平分线的性质
考点名称:角平分线的定义 考点名称:随机事件 考点名称:平行线的判定 考点名称:角平分线的性质
|

