 |
首页 > 考试 > 数学 > 初中数学 > 平行线的判定 > 正文 | 返回 打印 |
|
 |
首页 > 考试 > 数学 > 初中数学 > 平行线的判定 > 正文 | 返回 打印 |
|
答案
| 在同一平面内,过直线外一点有一条直线和已知直线平行,故(1)错误; 在同一平面内,过一点且只有一条直线和已知直线垂直,故(2)错误; 如图:  ∠ABC=∠DEF=90°,且∠ABC+∠DEF=180°,但是两角不是邻补角,故(3)错误; 同一平面内不平行的两条直线一定相交正确, 因为不特别指出时,一般认为,两条直线重合就是同一条直线,所以所提出的命题是正确的,故(4)正确. 即正确的个数是1个. 故选A. |
据专家权威分析,试题“下面说法正确的个数为()(1)过直线外一点有一条直线与已知直线平行..”主要考查你对 平行线的判定,平行线的性质,平行线的公理,垂直的判定与性质,相交线 等考点的理解。关于这些考点的“档案”如下:
平行线的判定平行线的性质,平行线的公理垂直的判定与性质相交线
考点名称:平行线的判定
平行线的判定平行线的判定公理:
(1)两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简称:同位角相等,两直线平行。
(2)两条直线被第三条直线所截,如果内错角相等,那么两直线平行。简称:内错角相等,两直线平行。
(3)两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。简称:同旁内角互补,两直线平行。
还有下面的判定方法:
(1)平行于同一条直线的两直线平行。
(2)垂直于同一条直线的两直线平行。
(3)平行线的定义。
判定方法的逆应用:
在同一平面内,两直线不相交,即平行。
两条直线平行于一条直线,则三条不重合的直线互相平行。
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
6a⊥c,b⊥c则a∥b。
考点名称:平行线的性质,平行线的公理
平行公理:过直线外一点有且只有一条直线与已知直线平行。
推论(平行线的传递性):平行同一直线的两直线平行。
∵a∥c,c ∥b
∴a∥b。
平行线的性质:
1. 两条平行被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
2. 两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等。
3 . 两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补。
考点名称:垂直的判定与性质
考点名称:相交线
相交线性质: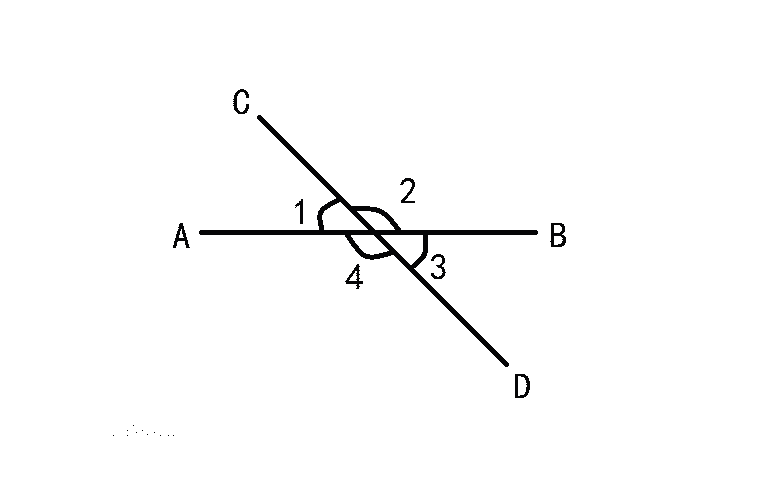
∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角。
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角。
∠1与∠2互补,∠3与∠2互补,由“同角的补角相等”,可以得出∠1=∠3.类似地,∠2=∠4.这样,
我们得到了对顶角的性质:对顶角相等。
垂线:
垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线,即:
过一点有且只有一条直线与已知直线垂直。
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。