|
题文
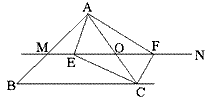
如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设直线MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F。
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF是正方形。 |
|
|
题型:解答题 难度:偏难
答案
解:(1)OE=OF 理由:∵CE平分∠ACB 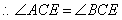
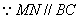 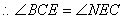 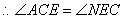 
同理:OC=OF OE=OF
(2)当点O运动到AC的中点处时,四边形AECF是矩形
理由: ∵AO=OC,OE=OF ∴四边形AECF是平行四边形
∵CE、CF分别是∠ACB、∠ACP平分线
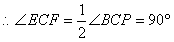
∴平行四边形AECF是矩形。
(3)在(2)的条件下,当△ABC满足条件 时,四边形AECF是正方形 时,四边形AECF是正方形
理由: , ,
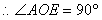 即 即
∴矩形AECF是正方形。 |
据专家权威分析,试题“如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设直线..”主要考查你对 平行线的性质,平行线的公理,矩形,矩形的性质,矩形的判定,正方形,正方形的性质,正方形的判定 等考点的理解。关于这些考点的“档案”如下:
平行线的性质,平行线的公理矩形,矩形的性质,矩形的判定正方形,正方形的性质,正方形的判定
考点名称:平行线的性质,平行线的公理 考点名称:矩形,矩形的性质,矩形的判定 考点名称:正方形,正方形的性质,正方形的判定
|

