题文
| 已知△ABC中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不重合)Q是BC边上的动点(与点B、C不重合). |
|

|
(1)如图,当PQ∥AC,且Q为BC的中点时,求线段CP的长;
(2)当PQ与AC不平行时,△CPQ可能为直角三角形吗?若有可能,请求出线段CQ的长的取值范围;若不可能,请说明理由. |
题型:解答题 难度:中档
答案
(1)在Rt△ABC中,∠ACB=90°,AC=5,BC=12
∴ AB=13. ∵ Q是BC的中点.
∴ CQ=QB.又∵ PQ∥AC. ∴ AP=PB,即P是AB的中点.
∴ Rt△ABC中,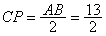 ; ;
(2)当AC与PQ不平行时,只有∠CPQ为直角,△CPQ才可能是直角三角形.
以CQ为直径作半圆D.
①当半圆D与AB相切时,设切点为M,连结DM,则 DM⊥AB,且AC=AM=5.
∴ MB=AB-AM=13-5=8.设CD=x,则DM=x,DB=12-x.
在Rt△DMB中,DB2=DM2+MB2.即 (12-x) 2=x 2+82.
解之得: ∴ CQ= ∴ CQ=  即当CQ 即当CQ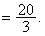 且点P运动到切点M位置时, 且点P运动到切点M位置时,
△CPQ为直角三角形.
②当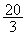 <CQ<12时,半圆D与直线AB有两个交点,当点P运动到这两个交点的位置时, <CQ<12时,半圆D与直线AB有两个交点,当点P运动到这两个交点的位置时,
△CPQ为直角三角形.
③当0<CQ<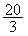 时,半圆D与直线AB相离,即点P在AB边上运动时,均在半圆D外,∠CPQ<90°. 时,半圆D与直线AB相离,即点P在AB边上运动时,均在半圆D外,∠CPQ<90°.
此时△CPQ不可能为直角三角形
∴ 当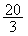 ≤CQ<12时,△CPQ可能为直角三角形. ≤CQ<12时,△CPQ可能为直角三角形. |
据专家权威分析,试题“已知△ABC中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不..”主要考查你对 平行线的性质,平行线的公理,勾股定理,直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离) 等考点的理解。关于这些考点的“档案”如下:
平行线的性质,平行线的公理勾股定理直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)
考点名称:平行线的性质,平行线的公理
考点名称:勾股定理
考点名称:直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)

