已知如图，AD是△ABC的角平分线，过点A的直线MN⊥AD，CH⊥MN。求证：HB+CH>AB+AC。-八年级数学打印页面

首页 > 考试 > 数学 > 初中数学 > 平行线的性质，平行线的公理 > 正文

已知如图，AD是△ABC的角平分线，过点A的直线MN⊥AD，CH⊥MN。求证：HB+CH>AB+AC。-八年级数学

[db:作者] 2020-01-06 00:00:00 零零社区

题文

已知如图，AD是△ABC的角平分线，过点A的直线MN⊥AD，CH⊥MN。求证：HB+CH>AB+AC。

题型：证明题难度：中档

答案

解：延长CH交BA的延长线于E

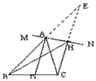
因为AD平分∠BAC，MN⊥AD，CH⊥MN
所以AD∥CH
所以∠BAD=∠E，∠DAC=∠ACH
由AN平分∠CAE，得∠BAD=∠DAC
故∠E=∠ACH
因为CH⊥MN，∠AHC=∠AHE=90°
因为AH=AH
所以△ACH≌△AEH
所以CH=EH
由CH⊥MN，易知MN是CE的垂直平分线
所以AC=AE
在△BHE中，BH+HE>BE，即BH+HC>BE，所以HB+CH>AB+AC。

据专家权威分析，试题“已知如图，AD是△ABC的角平分线，过点A的直线MN⊥AD，CH⊥MN。求证：..”主要考查你对平行线的性质，平行线的公理，全等三角形的性质，垂直平分线的性质等考点的理解。关于这些考点的“档案”如下：

平行线的性质，平行线的公理全等三角形的性质垂直平分线的性质

考点名称：平行线的性质，平行线的公理

平行公理：过直线外一点有且只有一条直线与已知直线平行。
推论（平行线的传递性）：平行同一直线的两直线平行。
∵a∥c，c ∥b
∴a∥b。

平行线的性质：
1. 两条平行被第三条直线所截，同位角相等。
简单说成：两直线平行，同位角相等。
2. 两条平行线被第三条直线所截，内错角相等。
简单说成：两直线平行，内错角相等。
3 . 两条平行线被第三条直线所截，同旁内角互补。
简单说成：两直线平行，同旁内角互补。
平行线的性质公理注意：
①注意条件“经过直线外一点”，若经过直线上一点作已知直线的平行线，就与已知直线重合了；
②平行公理体现了平行线的存在性和唯一性；
③平行公理的推论体现了平行线的传递性。
④在两直线平行的前提下才存在同位角相等、内错角相等、同旁内角互补的结论。这是平行线特有的性质。不要一提同位角或内错角就认为他们相等，一提同旁内角就认为互补，若没有两直线平行的条件，他们是不成立的。

考点名称：全等三角形的性质

全等三角形：
两个全等的三角形，而该两个三角形的三条边及三个角都对应地相等。全等三角形是几何中全等的一种。根据全等转换，两个全等三角形可以是平移、旋转、轴对称，或重叠等。当两个三角形的对应边及角都完全相对时，该两个三角形就是全等三角形。正常来说，验证两个全等三角形时都以三个相等部分来验证，最后便能得出结果。
全等三角形的对应边相等，对应角相等。
①全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边;
②全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角;
③有公共边的，公共边一定是对应边;
④有公共角的，角一定是对应角;
⑤有对顶角的，对顶角一定是对应角。
全等三角形的性质：
1.全等三角形的对应角相等。
2.全等三角形的对应边相等。
3.全等三角形的对应边上的高对应相等。
4.全等三角形的对应角的角平分线相等。
5.全等三角形的对应边上的中线相等。
6.全等三角形面积相等。
7.全等三角形周长相等。
8.全等三角形的对应角的三角函数值相等。

考点名称：垂直平分线的性质

垂直平分线的概念：
垂直于一条线段并且平分这条线段的直线，叫做这条线段的垂直平分线（中垂线）。
如图：直线MN即为线段AB的垂直平分线。
垂直平分线的性质：
1.垂直平分线垂直且平分其所在线段。
2.垂直平分线上任意一点，到线段两端点的距离相等。
逆定理：和一条线段两个端点距离相等的点，在这条线段的垂直平分线上。
3.如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线。
4.三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点的距离相等。
（此时以外心为圆心，外心到顶点的长度为半径，所作的圆为此三角形的外接圆。）

判定：
①利用定义；
②到一条线段两个端点距离相等的点，在这条线段的垂直平分线上。
（即线段垂直平分线可以看成到线段两端点距离相等的点的集合）
尺规作法：（用圆规作图）
1、在线段的中心找到这条线段的中点通过这个点做这条线段的垂线段。
2、分别以线段的两个端点为圆心，以大于线段的二分之一长度为半径画弧线。得到两个交点(两交点交与线段的异侧)。
3、连接这两个交点。
原理：等腰三角形的高垂直平分底边。

http://www.00-edu.com/ks/shuxue/2/151/2020-01-07/1935395.html十二生肖
十二星座