|
题文
(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上且CE=CA,试求∠DAE的度数。
(2)如果把第(1)题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?说明理由。
(3)如果把第(1)题中“∠BAC=90。”的条件改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC有怎样的大小关系? |
 |
题型:解答题 难度:偏难
答案
解:(1)∵AB=AC,∠BAC=90°
∴∠B=∠ACB=45°
∵BD=BA
∴∠BAD=∠BDA=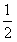 (180°-∠B)=67.5° (180°-∠B)=67.5°
∵CE=CA
∴∠CAE=∠E= ∠ACB=22.5° ∠ACB=22.5°
在△ABE中,∠BAE=180°-∠B-∠E=112.5°
∴∠DAE=∠BAE-∠BAD=112.5°-67.5°=45°
(2)不改变
设∠CAE=x
∵CA=CE
∴∠E=∠CAE=x
∴∠ACB=∠CAE+∠E=2x
在△ABC中,∠BAC=90°
∴∠B=90°-∠ACB=90°-2x
∵BD=BA
∴∠BAD=∠BDA= (180°-∠B)=x+45° (180°-∠B)=x+45°
在△ABE中,∠BAE=180°-∠B-∠E
=180°-(90°-2x)-x=90°+x
∴∠DAE=∠BAE-∠BAD
=(90°+x)-(x+45°)
=45°
(3)∠DAE= ∠BAC ∠BAC
理由:设∠CAE=x,∠BAD=y
则∠B=180°-2y,∠E=∠CAE=x
∴∠BAE=180°-∠B-∠E=2y-x
∴∠DAE=∠BAE-∠BAD=2y-x-y=y-x
∠BAC=∠BAE-∠CAE=2y-x-x=2y-2x
∴∠DAE= ∠BAC ∠BAC |
据专家权威分析,试题“(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在..”主要考查你对 三角形的内角和定理,等腰三角形的性质,等腰三角形的判定 等考点的理解。关于这些考点的“档案”如下:
三角形的内角和定理等腰三角形的性质,等腰三角形的判定
考点名称:三角形的内角和定理 考点名称:等腰三角形的性质,等腰三角形的判定
|

