零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 三角形的内角和定理 > 正文 返回　打印

如图，已知：在直角△ABC中，∠C=90°，BD平分∠ABC且交AC于D．（1）若∠BAC=30°，求证：AD=BD；（2）若AP平分∠BAC且交BD于P，求∠BPA的度数．-七年级数学
[db:作者]  2020-01-10 00:00:00  零零社区

题文

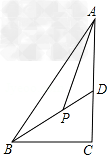
如图，已知：在直角△ABC中，∠C=90°，BD平分∠ABC且交AC于D．
（1）若∠BAC=30°，求证：AD=BD；
（2）若AP平分∠BAC且交BD于P，求∠BPA的度数．
题型：解答题  难度：中档

答案

（1）证明：∵∠BAC=30°，∠C=90°，
∴∠ABC=60°．
又∵BD平分∠ABC，
∴∠ABD=30°，
∴∠BAC=∠ABD，
∴BD=AD．
（2）解法一：∵∠C=90°，
∴∠BAC+∠ABC=90°，
∴（∠BAC+∠ABC）=45°．
∵BD平分∠ABC，AP平分∠BAC，
∠BAP=∠BAC，∠ABP=∠ABC，即∠BAP+∠ABP=45°
∴∠APB=180°﹣45°=135°．
解法二：∵∠C=90°，
∴∠BAC+∠ABC=90°，
∴（∠BAC+∠ABC）=45°．
∵BD平分∠ABC，AP平分∠BAC，
∠DBC=∠ABC，∠PAC=∠BAC，
∴∠DBC+∠PAD=45°．
∴∠BPA=∠PDA+∠PAD
=∠DBC+∠C+∠PAD
=∠DBC+∠PAD+∠C
=45°+90°
=135°．

据专家权威分析，试题“如图，已知：在直角△ABC中，∠C=90°，BD平分∠ABC且交AC于D．（1）若∠B..”主要考查你对  三角形的内角和定理，等腰三角形的性质，等腰三角形的判定  等考点的理解。关于这些考点的“档案”如下：

三角形的内角和定理等腰三角形的性质，等腰三角形的判定

考点名称：三角形的内角和定理

  • 三角形的内角和定理及推论：
    三角形的内角和定理：三角形三个内角和等于180°。
    推论：
    （1）直角三角形的两个锐角互余。
    （2）三角形的一个外角等于和它不相邻的来两个内角的和。
    （3）三角形的一个外角大于任何一个和它不相邻的内角。
    注：在同一个三角形中：等角对等边；等边对等角；大角对大边；大边对大角。

考点名称：等腰三角形的性质，等腰三角形的判定

  • 定义：
    有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。

  • 等腰三角形的性质：
    1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
    2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
    3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
    4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
    5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
    6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
    7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
    8.等腰三角形中腰的平方等于高的平方加底的一半的平方
    9.等腰三角形中腰大于高
    10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)

  • 等腰三角形的判定：
    1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
    2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
    3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。
http://www.00-edu.com/ks/shuxue/2/155/2020-01-10/1962313.html十二生肖
十二星座