如图，Rt△ABC中，CD是斜边AB上的高，角平分线AE交CD于H，EF⊥AB于F，有下列结论：①∠ACD=∠B；②CH=CE=EF；③AC=AF；④CH=HD；⑤BE=CH．其中你认为正确的有______．（填序号就可以）-数学打印页面

如图，Rt△ABC中，CD是斜边AB上的高，角平分线AE交CD于H，EF⊥AB于F，有下列结论：①∠ACD=∠B；②CH=CE=EF；③AC=AF；④CH=HD；⑤BE=CH．其中你认为正确的有______．（填序号就可以）-数学

[db:作者] 2020-01-10 00:00:00 互联网

题文

如图，Rt△ABC中，CD是斜边AB上的高，角平分线AE交CD于H，EF⊥AB于F，有下列结论：①∠ACD=∠B；②CH=CE=EF；③AC=AF；④CH=HD；⑤BE=CH．其中你认为正确的有______．（填序号就可以）

题型：填空题难度：中档

答案

①、∵CD是斜边AB上的高，∠ACB=90°，
∴∠CDB=90°，
∴∠ACD+∠BCD=90°，∠BCD+∠B=90°，
∴∠ACD=∠B，
∴①正确；
②、∵AE平分∠CAB，
∴∠CAE=∠BAE，
∵∠C=90°，EF⊥AB，
∴CE=FE，
∵∠CHE=∠CAE+ACD，∠CEA=∠BAE+∠B，
∵∠ACD=∠B，
∴∠CHE=∠CEA，
∴CH=CE，
即：CH=CE=EF，∴②正确；
③、∵在Rt△ACE和Rt△AFE中AE=AE，CE=EF，
∴Rt△ACE≌Rt△AFE，
∴AC=AF，∴③正确；
④、∵CH=EF，∴CH≠HD，∴④错误；
⑤、∵在Rt△BFE中，BE＞EF，而EF=CH，∴⑤错误；
故答案为：①②③．

据专家权威分析，试题“如图，Rt△ABC中，CD是斜边AB上的高，角平分线AE交CD于H，EF⊥AB于..”主要考查你对三角形的外角性质，等腰三角形的性质，等腰三角形的判定，角平分线的性质等考点的理解。关于这些考点的“档案”如下：

三角形的外角性质等腰三角形的性质，等腰三角形的判定角平分线的性质

考点名称：三角形的外角性质

三角形的外角：
三角形的一条边的延长线和另一条相邻的边组成的角，叫做三角形的外角。

∠1是三角形的外角。
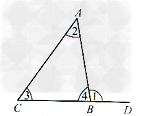
三角形的外角特征：
①顶点在三角形的一个顶点上，如∠ACD的顶点C是△ABC的一个顶点；
②一条边是三角形的一边，如∠ACD的一条边AC正好是△ABC的一条边；
③另一条边是三角形某条边的延长线如∠ACD的边CD是△ABC的BC边的延长线。

性质：
①. 三角形的外角与它相邻的内角互补。
②. 三角形的一个外角等于和它不相邻的两个内角的和。
③. 三角形的一个外角大于任何一个和它不相邻的内角。
④. 三角形的外角和等于360°。
设三角形ABC 则三个外角和=（A+B）+（A+C）+（B+C）=360度。

定理：三角形的一个外角等于不相邻的两个内角和。
定理：三角形的三个内角和为180度。

考点名称：等腰三角形的性质，等腰三角形的判定

定义：
有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。
等腰三角形的性质：
1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)
等腰三角形的判定：
1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。

考点名称：角平分线的性质

角平分线：
三角形的一个角的平分线与这个角的对边相交，连结这个角的顶点和与对边交点的线段叫做三角形的角平分线（也叫三角形的内角平分线）。由定义可知，三角形的角平分线是一条线段。由于三角形有三个内角，所以三角形有三条角平分线。三角形的角平分线交点一定在三角形内部。
角平方线定理：
①角平分线上的任意一点，到角两边的距离相等。垂直于两边为最短距离。
②角平分线能得到相同的两个角，都等于该角的一半。
③三角形三条角平分线相交于一点，并且这一点到三边的距离相等。
④三角形的三个角的角平分线相交于一点，这个点称为内心，即以此点为圆心可以在三角形内部画一个内切圆。
逆定理：
在角的内部，到角两边的距离相等的点在角平分线上。
角平分线作法：
在角AOB中，画角平分线

方法一：
1.以点O为圆心，以任意长为半径画弧，两弧交角AOB两边于点M，N。
2.分别以点M，N为圆心，以大于1/2MN的长度为半径画弧，两弧交于点P。
3.作射线OP。
则射线OP为角AOB的角平分线。
当然，角平分线的作法有很多种。下面再提供一种尺规作图的方法供参考。

方法二：
1.在两边OA、OB上分别截取OM、OA和ON、OB，且使得OM=ON，OA=OB；
2.连接AN与BM，他们相交于点P；
3.作射线OP。
则射线OP为角AOB的角平分线。

http://www.00-edu.com/ks/shuxue/2/156/2020-01-10/1960236.html十二生肖
十二星座