如图，在四边形ABCD中，AB∥CD，点E、F分别在AD、BC边上，连接AC交EF于G，∠1=∠BAC．（1）求证：EF∥CD；（2）若∠CAF=15°，∠2=45°，∠3=20°，求∠B和∠ACD的度数．-数学打印页面

如图，在四边形ABCD中，AB∥CD，点E、F分别在AD、BC边上，连接AC交EF于G，∠1=∠BAC．（1）求证：EF∥CD；（2）若∠CAF=15°，∠2=45°，∠3=20°，求∠B和∠ACD的度数．-数学

[db:作者] 2020-01-10 00:00:00 互联网

题文

如图，在四边形ABCD中，AB∥CD，点E、F分别在AD、BC边上，连接AC交EF于G，∠1=∠BAC．
（1）求证：EF∥CD；
（2）若∠CAF=15°，∠2=45°，∠3=20°，求∠B和∠ACD的度数．
题型：解答题难度：中档

答案

证明：（1）

如右图，
∵∠1=∠BAC，
∴AB∥EF，
∵AB∥CD，
∴EF∥CD；

（2）∵EF∥CD，
∴∠B+∠BFE=180°，
∵∠BFE=∠2+∠3=65°，
∴∠B=115°，
∵∠1是△AGF的外角，
∴∠1=∠3+∠GAF=35°，
∵EF∥CD，
∴∠ACD=∠1=35°．

据专家权威分析，试题“如图，在四边形ABCD中，AB∥CD，点E、F分别在AD、BC边上，连接AC交..”主要考查你对三角形的外角性质等考点的理解。关于这些考点的“档案”如下：

三角形的外角性质

考点名称：三角形的外角性质

三角形的外角：
三角形的一条边的延长线和另一条相邻的边组成的角，叫做三角形的外角。

∠1是三角形的外角。
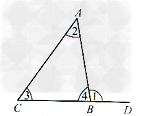
三角形的外角特征：
①顶点在三角形的一个顶点上，如∠ACD的顶点C是△ABC的一个顶点；
②一条边是三角形的一边，如∠ACD的一条边AC正好是△ABC的一条边；
③另一条边是三角形某条边的延长线如∠ACD的边CD是△ABC的BC边的延长线。

性质：
①. 三角形的外角与它相邻的内角互补。
②. 三角形的一个外角等于和它不相邻的两个内角的和。
③. 三角形的一个外角大于任何一个和它不相邻的内角。
④. 三角形的外角和等于360°。
设三角形ABC 则三个外角和=（A+B）+（A+C）+（B+C）=360度。

定理：三角形的一个外角等于不相邻的两个内角和。
定理：三角形的三个内角和为180度。

http://www.00-edu.com/ks/shuxue/2/156/2020-01-10/1960724.html十二生肖
十二星座