|
题文
题型:解答题 难度:中档
答案
解:(1)当然是GH不变,
重心是三角形中线交点,它把中线分为1:2的比例,
如果中线长度不变,题中的三线段长度也不变,PO是半径,
它是直角三角形OPH的斜边,它的中线等于它的一半;
则GH= ( ( OP)= OP)=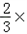 ( (  ×6)=2; ×6)=2;
(2)延长OG交PH于点K,
∵△PGH为Rt△ FG=1,PF=3,
∴PG=2 , ,
∴PH= , ,
∴KG=
∴OG=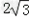
∴OG:PG:HG= :2 :2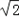 :2= :2= : : :1; :1;
(3)△PGH是等腰三角形有3种可能性,
①当GP=PH时,PH=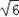 , ,
②当GP=GH时,PH=0(不存在),
③当PH=GH时,PH=2,
∴PH=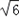 或PH=2. 或PH=2. |
 |
据专家权威分析,试题“如图,在半径为6,圆心角为90°的扇形OAB的上,有一个动点P,PH⊥O..”主要考查你对 三角形的内心、外心、中心、重心,等腰三角形的性质,等腰三角形的判定,勾股定理 等考点的理解。关于这些考点的“档案”如下:
三角形的内心、外心、中心、重心等腰三角形的性质,等腰三角形的判定勾股定理
考点名称:三角形的内心、外心、中心、重心 考点名称:等腰三角形的性质,等腰三角形的判定 考点名称:勾股定理
|

