零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 三角形的内心、外心、中心、重心 > 正文 返回　打印

已知△ABC（如图所示）．（1）在图中找出重心O；（2）设BC，AC，AB边的中点为M，N，G，度量OM和OA，ON与OB，OG与OC，根据度量的结果，猜想三角形的重心到三角形顶点的距离与到对边中-八年级数学
[db:作者]  2020-01-14 00:00:00  零零社区

题文

已知△ABC（如图所示）．
（1）在图中找出重心O；
（2）设BC，AC，AB边的中点为M，N，G，度量OM和OA，ON与OB，OG与OC，根据度量的结果，猜想三角形的重心到三角形顶点的距离与到对边中点的距离之间的距离，并给予证明．
题型：解答题  难度：中档

答案

解：（1）用尺规作图作出△ABC三边的中线AM，BN，CG，设它们的交点为O，则O为△ABC的重心
（2）通过度量发现：AO=2OM，BO=2ON，CO=2OG
猜想：三角形的重心O到三角形顶点的距离等于它到对边中点的距离的两倍．
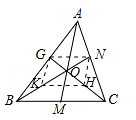
证明：如图所示，取BO，CO的中点K，H，连接KH，HN，NG，G，
∵G，N分别是AB，AC的中点，
∴GN平行且等于 BC．
又∵K，H分别是OB，OC边的中点，
∴KH平行且等于 BC．
∴GN平行且等于KH．
∴四边形KHNG是平行四边形．
∴GO=OH，NO=KO．
而BK=KO，CH=HO，
∴BO=2ON，CO=2OG．
若取AO的中点R，同理，可证AO=2OM．
∴AO=2OM，BO=2ON，CO=2OG．

据专家权威分析，试题“已知△ABC（如图所示）．（1）在图中找出重心O；（2）设BC，AC，AB边的中..”主要考查你对  三角形的内心、外心、中心、重心，三角形中位线定理，平行四边形的性质  等考点的理解。关于这些考点的“档案”如下：

三角形的内心、外心、中心、重心三角形中位线定理平行四边形的性质

考点名称：三角形的内心、外心、中心、重心

  • 三角形的四心定义：
    1、内心：三角形三条内角平分线的交点，即内切圆的圆心。
    内心是三角形角平分线交点的原理：经圆外一点作圆的两条切线，这一点与圆心的连线平分两条切线的夹角（原理：角平分线上点到角两边距离相等）。
    2、外心：是三角形三条边的垂直平分线的交点，即外接圆的圆心。
    外心定理：三角形的三边的垂直平分线交于一点。该点叫做三角形的外心。
    3、中心：三角形只有五种心重心、垂心、内心、外心、旁心，当且仅当三角形是正三角形的时候，四心合一心，称做正三角形的中心。
    4、重心：重心是三角形三边中线的交点。

  • 三角形的外心的性质：
    1.三角形三条边的垂直平分线的交于一点，该点即为三角形外接圆的圆心；
    2三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合；
    3.锐角三角形的外心在三角形内；
    钝角三角形的外心在三角形外；
    直角三角形的外心与斜边的中点重合。

    在△ABC中
    4.OA=OB=OC=R
    5.∠BOC=2∠BAC，∠AOB=2∠ACB，∠COA=2∠CBA
    6.S△ABC=abc/4R

    三角形的内心的性质：
    1.三角形的三条角平分线交于一点，该点即为三角形的内心
    2.三角形的内心到三边的距离相等，都等于内切圆半径r
    3.r=2S/(a+b+c)
    4.在Rt△ABC中，∠C=90°，r=(a+b-c)/2．
    5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/2
    6.S△=[(a+b+c)r]/2 (r是内切圆半径)

    三角形的垂心的性质:
    1.锐角三角形的垂心在三角形内；
    直角三角形的垂心在直角顶点上；
    钝角三角形的垂心在三角形外。
    2.三角形的垂心是它垂足三角形的内心；或
    者说，三角形的内心是它旁心三角形的垂心。

    例如在△ABC中
    3. 垂心O关于三边的对称点，均在△ABC的外接圆圆上。
    4.△ABC中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AO?OD=BO?OE=CO?OF
    5. H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
    6.△ABC，△ABO，△BCO，△ACO的外接圆是等圆。
    7.在非直角三角形中，过O的直线交AB、AC所在直线分别于P、Q，则 AB/AP?tanB+ AC/AQ?tanC=tanA+tanB+tanC
    8.三角形任一顶点到垂心的距离，等于外心到对边的距离的2倍。
    9.设O，H分别为△ABC的外心和垂心，则∠BAO=∠HAC，∠ABH=∠OBC，∠BCO=∠HCA。
    10.锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
    11.锐角三角形的垂心是垂足三角形的内心；锐角三角形的内接三角形(顶点在原三角形的边上)中，以垂足三角形的周长最短。
    12.西姆松(Simson)定理（西姆松线）：从一点向三角形的三边所引垂线的垂足共线的重要条件是该点落在三角形的外接圆上
    13.设锐角△ABC内有一点P，那么P是垂心的充分必要条件是PB?PC?BC+PB?PA?AB+PA?PC?AC=AB?BC?CA。
    14.设H为非直角三角形的垂心，且D、E、F分别为H在BC，CA，AB上的射影，H1，H2，H3分别为△AEF，△BDF，△CDE的垂心，则△DEF≌△H1H2H3。
    15.三角形垂心H的垂足三角形的三边，分别平行于原三角形外接圆在各顶点的切线。

    三角形的重心的性质:
    1.重心到顶点的距离与重心到对边中点的距离之比为2：1。
    2.重心和三角形3个顶点组成的3个三角形面积相等。
    3.重心到三角形3个顶点距离的平方和最小。
    4.在平面直角坐标系中，重心的坐标是顶点坐标的算术平均，即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)；
    空间直角坐标系——横坐标：(X1+X2+X3)/3  纵坐标：(Y1+Y2+Y3)/3  竖坐标：（Z1+Z2+Z3）/3
    5.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
    6.重心是三角形内到三边距离之积最大的点。

    三角形旁心的性质:
    1、三角形一内角平分线和另外两顶点处的外角平分线交于一点，该点即为三角形的旁心。
    2、每个三角形都有三个旁心。
    3、旁心到三边的距离相等。
    三角形任意两角的外角平分线和第三个角的内角平分线的交点。一个三角形有三个旁心，而且一定在三角形外。

考点名称：三角形中位线定理

  • 三角形中位线定义：
    连接三角形两边中点的线段叫做三角形的中位线。一个三角形共有三条中位线。
    三角形中位线定理：
    三角形的中位线平行于第三边，并且等于它的一半。

    如图已知△ABC中，D，E分别是AB，AC两边中点。
    则DE平行于BC且等于BC/2

  • 三角形中位线逆定理：

    逆定理一：在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线。
    如图DE//BC，DE=BC/2，则D是AB的中点，E是AC的中点。
    逆定理二：在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线。
    如图D是AB的中点，DE//BC，则E是AC的中点，DE=BC/2

  • 区分三角形的中位线和中线：
    三角形的中位线是连结三角形两边中点的线段；
    三角形的中线是连结一个顶点和它的对边中点的线段。

考点名称：平行四边形的性质

  • 平行四边形的概念：
    两组对边分别平行的四边形叫做平行四边形。
    平行四边形用符号“□ABCD，如平行四边形ABCD记作“□ABCD”，读作ABCD”。
    ①平行四边形属于平面图形。
    ②平行四边形属于四边形。
    ③平行四边形中还包括特殊的平行四边形：矩形，正方形和菱形等。
    ④平行四边形属于中心对称图形。

  • 平行四边形的性质：
    主要性质
    （矩形、菱形、正方形都是特殊的平行四边形。）
    （1）如果一个四边形是平行四边形，那么这个四边形的两组对边分别相等。
    （简述为“平行四边形的两组对边分别相等”）
    （2）如果一个四边形是平行四边形，那么这个四边形的两组对角分别相等。
    （简述为“平行四边形的两组对角分别相等”）
    （3）如果一个四边形是平行四边形，那么这个四边形的邻角互补
    （简述为“平行四边形的邻角互补”）
    （4）夹在两条平行线间的平行线段相等。
    （5）如果一个四边形是平行四边形，那么这个四边形的两条对角线互相平分。
    （简述为“平行四边形的对角线互相平分”）
    （6）连接任意四边形各边的中点所得图形是平行四边形。(推论）
    （7）平行四边形的面积等于底和高的积。（可视为矩形）
    （8）过平行四边形对角线交点的直线，将平行四边形分成全等的两部分图形。
    （9）平行四边形是中心对称图形，对称中心是两对角线的交点.
    （10）平行四边形不是轴对称图形，矩形和菱形是轴对称图形。
    注：正方形，矩形以及菱形也是一种特殊的平行四边形，三者具有平行四边形的性质。

    （11）平行四边形ABCD中（如图）E为AB的中点，则AC和DE互相三等分，一般地，若E为AB上靠近A的n等分点，则AC和DE互相(n+1)等分。
    （12）平行四边形ABCD中，AC、BD是平行四边形ABCD的对角线，则各四边的平方和等于对角线的平方和。
    （13）平行四边形对角线把平行四边形面积分成四等分。
    （14）平行四边形中，两条在不同对边上的高所组成的夹角，较小的角等于平行四边形中较小的角，较大的角等于平行四边形中较大的角。
    （15）平行四边形中,一个角的顶点向他对角的两边所做的高，与这个角的两边组成的夹角相等。
http://www.00-edu.com/ks/shuxue/2/159/2020-01-14/1969000.html十二生肖
十二星座