零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 三角形的内心、外心、中心、重心 > 正文 返回　打印

已知某三角形的边长分别是3cm、4cm、5cm，则它的外接圆半径是______cm．-数学
[db:作者]  2020-01-14 00:00:00  零零社区

题文

已知某三角形的边长分别是3cm、4cm、5cm，则它的外接圆半径是______cm．
题型：填空题  难度：中档

答案




∵AC2+BC2=32+42=25，AB2=52=25，
∴AC2+BC2=AB2，
∴∠C=90°，
即△ABC是直角三角形，
∴△ABC的外接圆的半径是
1
2
AB=2.5，
故答案为：2.5．

据专家权威分析，试题“已知某三角形的边长分别是3cm、4cm、5cm，则它的外接圆半径是___..”主要考查你对  三角形的内心、外心、中心、重心，勾股定理的逆定理  等考点的理解。关于这些考点的“档案”如下：

三角形的内心、外心、中心、重心勾股定理的逆定理

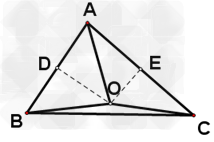
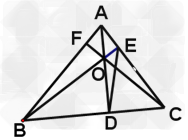
考点名称：三角形的内心、外心、中心、重心

  • 三角形的四心定义：
    1、内心：三角形三条内角平分线的交点，即内切圆的圆心。
    内心是三角形角平分线交点的原理：经圆外一点作圆的两条切线，这一点与圆心的连线平分两条切线的夹角（原理：角平分线上点到角两边距离相等）。
    2、外心：是三角形三条边的垂直平分线的交点，即外接圆的圆心。
    外心定理：三角形的三边的垂直平分线交于一点。该点叫做三角形的外心。
    3、中心：三角形只有五种心重心、垂心、内心、外心、旁心，当且仅当三角形是正三角形的时候，四心合一心，称做正三角形的中心。
    4、重心：重心是三角形三边中线的交点。

  • 三角形的外心的性质：
    1.三角形三条边的垂直平分线的交于一点，该点即为三角形外接圆的圆心；
    2三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合；
    3.锐角三角形的外心在三角形内；
    钝角三角形的外心在三角形外；
    直角三角形的外心与斜边的中点重合。

    在△ABC中
    4.OA=OB=OC=R
    5.∠BOC=2∠BAC，∠AOB=2∠ACB，∠COA=2∠CBA
    6.S△ABC=abc/4R

    三角形的内心的性质：
    1.三角形的三条角平分线交于一点，该点即为三角形的内心
    2.三角形的内心到三边的距离相等，都等于内切圆半径r
    3.r=2S/(a+b+c)
    4.在Rt△ABC中，∠C=90°，r=(a+b-c)/2．
    5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/2
    6.S△=[(a+b+c)r]/2 (r是内切圆半径)

    三角形的垂心的性质:
    1.锐角三角形的垂心在三角形内；
    直角三角形的垂心在直角顶点上；
    钝角三角形的垂心在三角形外。
    2.三角形的垂心是它垂足三角形的内心；或
    者说，三角形的内心是它旁心三角形的垂心。

    例如在△ABC中
    3. 垂心O关于三边的对称点，均在△ABC的外接圆圆上。
    4.△ABC中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AO?OD=BO?OE=CO?OF
    5. H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
    6.△ABC，△ABO，△BCO，△ACO的外接圆是等圆。
    7.在非直角三角形中，过O的直线交AB、AC所在直线分别于P、Q，则 AB/AP?tanB+ AC/AQ?tanC=tanA+tanB+tanC
    8.三角形任一顶点到垂心的距离，等于外心到对边的距离的2倍。
    9.设O，H分别为△ABC的外心和垂心，则∠BAO=∠HAC，∠ABH=∠OBC，∠BCO=∠HCA。
    10.锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
    11.锐角三角形的垂心是垂足三角形的内心；锐角三角形的内接三角形(顶点在原三角形的边上)中，以垂足三角形的周长最短。
    12.西姆松(Simson)定理（西姆松线）：从一点向三角形的三边所引垂线的垂足共线的重要条件是该点落在三角形的外接圆上
    13.设锐角△ABC内有一点P，那么P是垂心的充分必要条件是PB?PC?BC+PB?PA?AB+PA?PC?AC=AB?BC?CA。
    14.设H为非直角三角形的垂心，且D、E、F分别为H在BC，CA，AB上的射影，H1，H2，H3分别为△AEF，△BDF，△CDE的垂心，则△DEF≌△H1H2H3。
    15.三角形垂心H的垂足三角形的三边，分别平行于原三角形外接圆在各顶点的切线。

    三角形的重心的性质:
    1.重心到顶点的距离与重心到对边中点的距离之比为2：1。
    2.重心和三角形3个顶点组成的3个三角形面积相等。
    3.重心到三角形3个顶点距离的平方和最小。
    4.在平面直角坐标系中，重心的坐标是顶点坐标的算术平均，即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)；
    空间直角坐标系——横坐标：(X1+X2+X3)/3  纵坐标：(Y1+Y2+Y3)/3  竖坐标：（Z1+Z2+Z3）/3
    5.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
    6.重心是三角形内到三边距离之积最大的点。

    三角形旁心的性质:
    1、三角形一内角平分线和另外两顶点处的外角平分线交于一点，该点即为三角形的旁心。
    2、每个三角形都有三个旁心。
    3、旁心到三边的距离相等。
    三角形任意两角的外角平分线和第三个角的内角平分线的交点。一个三角形有三个旁心，而且一定在三角形外。

考点名称：勾股定理的逆定理

  • 勾股定理的逆定理:
    如果三角形的三边长a，b，c满足，那么这个三角形是直角三角形。

    勾股定理的逆定理是判断三角形为锐角或钝角的一个简单的方法。
    若c为最长边，且a2+b2=c2，则△ABC是直角三角形。如果a2+b2>c2，则△ABC是锐角三角形。如果a2+b2<c2，则△ABC是钝角三角形。
    由于余弦定理是由勾股定理推出的，故可以用来证明其逆定理而不算循环论证。
    勾股定理的逆定理是判定三角形是不是直角三角形的重要方法。

  • 勾股定理的来源：
    毕达哥拉斯树是一个基本的几何定理，传统上认为是由古希腊的毕达哥拉斯所证明。据说毕达哥拉斯证明了这个定理后，即斩了百头牛作庆祝，因此又称“百牛定理”。
    毕达哥拉斯在中国，《周髀算经》记载了勾股定理的公式与证明，相传是在商代由商高发现，故又有称之为商高定理；三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释，又给出了另外一个证明。法国和比利时称为驴桥定理，埃及称为埃及三角形。中国古代把直角三角形中较短的直角边叫做勾，较长的直角边叫做股，斜边叫做弦。　
    常用勾股数组（3,4,5）；（6,8,10）；（5,12,13）；（8,15,17） ；（7,24,25）
    有关勾股定理书籍 ：《数学原理》人民教育出版社；《探究勾股定理》同济大学出版社；《优因培教数学》北京大学出版社；《勾股书籍》新世纪出版社；《九章算术一书》《优因培揭秘勾股定理》江西教育出版社；《几何原本》（原著：欧几里得）人民日报出版社。

    毕达哥拉斯树
    毕达哥拉斯树是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的图形。又因为重复数次后 的形状好似一棵树，所以被称为毕达哥拉斯树。　
    直角三角形两个直角边平方的和等于斜边的平方。两个相邻的小正方形面积的和等于相邻的一个大正方形的面积。利用不等式A2+B2≥2AB可以证明下面的结论：三个正方形之间的三角形，其面积小于等于大正方形面积的四分之一，大于等于一个小正方形面积的二分之一。
http://www.00-edu.com/ks/shuxue/2/159/2020-01-14/1969282.html十二生肖
十二星座