如图，等边△ABC，G是△ABC的重心，直线AG把△ABC分成面积相等的两部分，但是不是过G点的任意一条直线都把△ABC分成面积相等的两部分？用实验或说理的方法，给予探索并得出结论．-数学打印页面

首页 > 考试 > 数学 > 初中数学 > 三角形的内心、外心、中心、重心 > 正文

如图，等边△ABC，G是△ABC的重心，直线AG把△ABC分成面积相等的两部分，但是不是过G点的任意一条直线都把△ABC分成面积相等的两部分？用实验或说理的方法，给予探索并得出结论．-数学

[db:作者] 2020-01-14 00:00:00 零零社区

题文

如图，等边△ABC，G是△ABC的重心，直线AG把△ABC分成面积相等的两部分，但是不是过G点的任意一条直线都把△ABC分成面积相等的两部分？用实验或说理的方法，给予探索并得出结论．
题型：解答题难度：中档

答案

不是．
理由：如图，过G作直线EF∥AB，交AC于E、BC于F，
设直线AG与BC的交点为M，过M作MN∥EF，交AC于N．
∵G是△ABC的内心，
∴BM=MC，AG=2GM．
∵GE∥MN，
∴
AE
AN
=
AG
AM
=
2
3
，即AE=
2
3
AN．
∵BM=MC，即M是BC的中点，且MN∥EF∥AB，
∴MN是△ABC的中位线，即AN=NC．
∴AE=
2
3
AN=
2
3
NC．
设AE=2x，则AN=NC=3x，EN=x，
∴EC=NC+EN=4x，AC=AE+EC=6x．
∵EF∥AB，
∴△CMN∽△CBA，
∴
S△CMN
S△CBA
=（
EC
AC
）²=
4
9
，
故S_△CEF：S_{四边形AEFB}=4：5．
因此过G点的任意一条直线不是都能把△ABC分成面积相等的两部分．

据专家权威分析，试题“如图，等边△ABC，G是△ABC的重心，直线AG把△ABC分成面积相等的两部..”主要考查你对三角形的内心、外心、中心、重心，等边三角形，三角形的周长和面积等考点的理解。关于这些考点的“档案”如下：

三角形的内心、外心、中心、重心等边三角形三角形的周长和面积

考点名称：三角形的内心、外心、中心、重心

三角形的四心定义：
1、内心：三角形三条内角平分线的交点，即内切圆的圆心。
内心是三角形角平分线交点的原理：经圆外一点作圆的两条切线，这一点与圆心的连线平分两条切线的夹角（原理：角平分线上点到角两边距离相等）。
2、外心：是三角形三条边的垂直平分线的交点，即外接圆的圆心。
外心定理：三角形的三边的垂直平分线交于一点。该点叫做三角形的外心。
3、中心：三角形只有五种心重心、垂心、内心、外心、旁心，当且仅当三角形是正三角形的时候，四心合一心，称做正三角形的中心。
4、重心：重心是三角形三边中线的交点。
三角形的外心的性质：
1.三角形三条边的垂直平分线的交于一点，该点即为三角形外接圆的圆心；
2三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合；
3.锐角三角形的外心在三角形内；
钝角三角形的外心在三角形外；
直角三角形的外心与斜边的中点重合。

在△ABC中
4.OA=OB=OC=R
5.∠BOC=2∠BAC，∠AOB=2∠ACB，∠COA=2∠CBA
6.S△ABC=abc/4R

三角形的内心的性质：
1.三角形的三条角平分线交于一点，该点即为三角形的内心
2.三角形的内心到三边的距离相等，都等于内切圆半径r
3.r=2S/(a+b+c)
4.在Rt△ABC中，∠C=90°，r=(a+b-c)/2．
5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/2
6.S△=[(a+b+c)r]/2 (r是内切圆半径)

三角形的垂心的性质:
1.锐角三角形的垂心在三角形内；
直角三角形的垂心在直角顶点上；
钝角三角形的垂心在三角形外。
2.三角形的垂心是它垂足三角形的内心；或
者说，三角形的内心是它旁心三角形的垂心。

例如在△ABC中
3. 垂心O关于三边的对称点，均在△ABC的外接圆圆上。
4.△ABC中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AO?OD=BO?OE=CO?OF
5. H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
6.△ABC，△ABO，△BCO，△ACO的外接圆是等圆。
7.在非直角三角形中，过O的直线交AB、AC所在直线分别于P、Q，则 AB/AP?tanB+ AC/AQ?tanC=tanA+tanB+tanC
8.三角形任一顶点到垂心的距离，等于外心到对边的距离的2倍。
9.设O，H分别为△ABC的外心和垂心，则∠BAO=∠HAC，∠ABH=∠OBC，∠BCO=∠HCA。
10.锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
11.锐角三角形的垂心是垂足三角形的内心；锐角三角形的内接三角形(顶点在原三角形的边上)中，以垂足三角形的周长最短。
12.西姆松(Simson)定理（西姆松线）：从一点向三角形的三边所引垂线的垂足共线的重要条件是该点落在三角形的外接圆上
13.设锐角△ABC内有一点P，那么P是垂心的充分必要条件是PB?PC?BC+PB?PA?AB+PA?PC?AC=AB?BC?CA。
14.设H为非直角三角形的垂心，且D、E、F分别为H在BC，CA，AB上的射影，H1，H2，H3分别为△AEF，△BDF，△CDE的垂心，则△DEF≌△H1H2H3。
15.三角形垂心H的垂足三角形的三边，分别平行于原三角形外接圆在各顶点的切线。

三角形的重心的性质:
1.重心到顶点的距离与重心到对边中点的距离之比为2：1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
3.重心到三角形3个顶点距离的平方和最小。
4.在平面直角坐标系中，重心的坐标是顶点坐标的算术平均，即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)；
空间直角坐标系——横坐标：(X1+X2+X3)/3 纵坐标：(Y1+Y2+Y3)/3 竖坐标：（Z1+Z2+Z3）/3
5.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
6.重心是三角形内到三边距离之积最大的点。

三角形旁心的性质:
1、三角形一内角平分线和另外两顶点处的外角平分线交于一点，该点即为三角形的旁心。
2、每个三角形都有三个旁心。
3、旁心到三边的距离相等。
三角形任意两角的外角平分线和第三个角的内角平分线的交点。一个三角形有三个旁心，而且一定在三角形外。

考点名称：等边三角形

等边三角形定义：
三条边都相等的三角形叫做等边三角形，“等边三角形”也被称为“正三角形”。是特殊的等腰三角形。
如果一个三角形满足下列任意一条，则它必满足另一条，三边相等或三角相等的三角形叫做等边三角形：
1.三边长度相等；
2.三个内角度数均为60度；
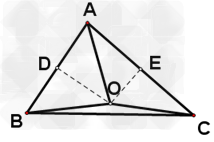
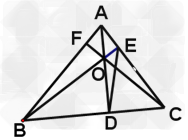
3.一个内角为60度的等腰三角形。
性质：
①等边三角形是锐角三角形，等边三角形的内角都相等，且均为60°。
②等边三角形每条边上的中线、高线和所对角的平分线互相重合（三线合一）
③等边三角形是轴对称图形，它有三条对称轴，对称轴是每条边上的中线、高线或对角的平分线所在的直线。
④等边三角形重心、内心、外心、垂心重合于一点，称为等边三角形的中心。（四心合一）
⑤等边三角形内任意一点到三边的距离之和为定值(等于其高)
判定方法：
①三边相等的三角形是等边三角形（定义）
②三个内角都相等（为60度）的三角形是等边三角形
③有一个角是60度的等腰三角形是等边三角形
④ 两个内角为60度的三角形是等边三角形
说明:可首先考虑判断三角形是等腰三角形。

等边三角形的性质与判定理解：
首先，明确等边三角形定义。三边相等的三角形叫做等边三角形，也称正三角形。
其次，明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形，等腰三角形不一定是等边三角形。

等比三角形的尺规做法：
可以利用尺规作图的方式画出正三角形，其作法相当简单：先用尺画出一条任意长度的线段（这条线段的长度决定等边三角形的边长），再分别以线段二端点为圆心、线段为半径画圆，二圆汇交于二点，任选一点，和原来线段的两个端点画线段，则这二条线段和原来线段即构成一正三角形。

考点名称：三角形的周长和面积

三角形的概念：
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

构成三角形的元素：
边：组成三角形的线段叫做三角形的边；
顶点：相邻两边的公共端点叫做三角形的顶点；
内角：相邻两边所组成的角叫做三角形的内角，简称三角形的角。

三角形有下面三个特性：
（1）三角形有三条线段；
（2）三条线段不在同一直线上；
（3）首尾顺次相接。

三角形的表示：
用符号“△，顶点是A、B、C的三角形记作“△ABC”，读作ABC”。
三角形的分类：
（1）三角形按边的关系分类如下：
；
（2）三角形按角的关系分类如下：

把边和角联系在一起，我们又有一种特殊的三角形：等腰直角三角形。它是两条直角边相等的直角三角形。
三角形的周长和面积：
三角形的周长等于三角形三边之和。
三角形面积=（底×高）÷2。

http://www.00-edu.com/ks/shuxue/2/159/2020-01-14/1969405.html十二生肖
十二星座