零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 三角形的内心、外心、中心、重心 > 正文 返回　打印

如图，已知⊙O是△ABC的外接圆，∠ACB=45°，∠ABC=120°，延长CB到D，使DB=2BC，连接AD，求证：AD切⊙O于点A．-数学
[db:作者]  2020-01-14 00:00:00  互联网

题文

如图，已知⊙O是△ABC的外接圆，∠ACB=45°，∠ABC=120°，延长CB到D，使DB=2BC，连接AD，求证：AD切⊙O于点A．

题型：解答题  难度：中档

答案



证明：如图：连接OA，OB，OC，且OB交AC于E，
∵∠ACB=45°，∠ABC=120°，∴∠AOB=90°，∠E0C=∠ECO=∠OAE=30°，
在直角△AOE中，设OE=a，则AE=2a，EC=a，
∴
EC
AE
=
a
2a
=
1
2
，
又∵DB=2BC，∴
BC
DB
=
1
2
．
∴
EC
AE
=
BC
DB
=
1
2
，
∴OB∥AD，
∴∠OAD=∠AOB=90°．
所以AD切⊙O于点A．

据专家权威分析，试题“如图，已知⊙O是△ABC的外接圆，∠ACB=45°，∠ABC=120°，延长CB到D，..”主要考查你对  三角形的内心、外心、中心、重心，直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）  等考点的理解。关于这些考点的“档案”如下：

三角形的内心、外心、中心、重心直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）

考点名称：三角形的内心、外心、中心、重心

  • 三角形的四心定义：
    1、内心：三角形三条内角平分线的交点，即内切圆的圆心。
    内心是三角形角平分线交点的原理：经圆外一点作圆的两条切线，这一点与圆心的连线平分两条切线的夹角（原理：角平分线上点到角两边距离相等）。
    2、外心：是三角形三条边的垂直平分线的交点，即外接圆的圆心。
    外心定理：三角形的三边的垂直平分线交于一点。该点叫做三角形的外心。
    3、中心：三角形只有五种心重心、垂心、内心、外心、旁心，当且仅当三角形是正三角形的时候，四心合一心，称做正三角形的中心。
    4、重心：重心是三角形三边中线的交点。

  • 三角形的外心的性质：
    1.三角形三条边的垂直平分线的交于一点，该点即为三角形外接圆的圆心；
    2三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合；
    3.锐角三角形的外心在三角形内；
    钝角三角形的外心在三角形外；
    直角三角形的外心与斜边的中点重合。

    在△ABC中
    4.OA=OB=OC=R
    5.∠BOC=2∠BAC，∠AOB=2∠ACB，∠COA=2∠CBA
    6.S△ABC=abc/4R

    三角形的内心的性质：
    1.三角形的三条角平分线交于一点，该点即为三角形的内心
    2.三角形的内心到三边的距离相等，都等于内切圆半径r
    3.r=2S/(a+b+c)
    4.在Rt△ABC中，∠C=90°，r=(a+b-c)/2．
    5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/2
    6.S△=[(a+b+c)r]/2 (r是内切圆半径)

    三角形的垂心的性质:
    1.锐角三角形的垂心在三角形内；
    直角三角形的垂心在直角顶点上；
    钝角三角形的垂心在三角形外。
    2.三角形的垂心是它垂足三角形的内心；或
    者说，三角形的内心是它旁心三角形的垂心。

    例如在△ABC中
    3. 垂心O关于三边的对称点，均在△ABC的外接圆圆上。
    4.△ABC中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AO?OD=BO?OE=CO?OF
    5. H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
    6.△ABC，△ABO，△BCO，△ACO的外接圆是等圆。
    7.在非直角三角形中，过O的直线交AB、AC所在直线分别于P、Q，则 AB/AP?tanB+ AC/AQ?tanC=tanA+tanB+tanC
    8.三角形任一顶点到垂心的距离，等于外心到对边的距离的2倍。
    9.设O，H分别为△ABC的外心和垂心，则∠BAO=∠HAC，∠ABH=∠OBC，∠BCO=∠HCA。
    10.锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
    11.锐角三角形的垂心是垂足三角形的内心；锐角三角形的内接三角形(顶点在原三角形的边上)中，以垂足三角形的周长最短。
    12.西姆松(Simson)定理（西姆松线）：从一点向三角形的三边所引垂线的垂足共线的重要条件是该点落在三角形的外接圆上
    13.设锐角△ABC内有一点P，那么P是垂心的充分必要条件是PB?PC?BC+PB?PA?AB+PA?PC?AC=AB?BC?CA。
    14.设H为非直角三角形的垂心，且D、E、F分别为H在BC，CA，AB上的射影，H1，H2，H3分别为△AEF，△BDF，△CDE的垂心，则△DEF≌△H1H2H3。
    15.三角形垂心H的垂足三角形的三边，分别平行于原三角形外接圆在各顶点的切线。

    三角形的重心的性质:
    1.重心到顶点的距离与重心到对边中点的距离之比为2：1。
    2.重心和三角形3个顶点组成的3个三角形面积相等。
    3.重心到三角形3个顶点距离的平方和最小。
    4.在平面直角坐标系中，重心的坐标是顶点坐标的算术平均，即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)；
    空间直角坐标系——横坐标：(X1+X2+X3)/3  纵坐标：(Y1+Y2+Y3)/3  竖坐标：（Z1+Z2+Z3）/3
    5.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
    6.重心是三角形内到三边距离之积最大的点。

    三角形旁心的性质:
    1、三角形一内角平分线和另外两顶点处的外角平分线交于一点，该点即为三角形的旁心。
    2、每个三角形都有三个旁心。
    3、旁心到三边的距离相等。
    三角形任意两角的外角平分线和第三个角的内角平分线的交点。一个三角形有三个旁心，而且一定在三角形外。

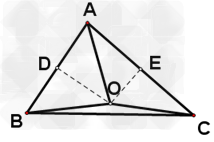
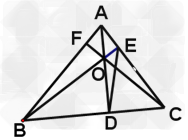
考点名称：直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）

  • 直线与圆的位置关系:
    直线与圆的位置关系有三种：直线与圆相交，直线与圆相切，直线与圆相离。
    （1）相交：直线和圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线，公共点叫做交点AB与⊙O相交，d<r；
    （2）相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线，这个唯一的公共点叫做切点。AB与⊙O相切，d=r。
    （3）相离：直线和圆没有公共点时，叫做直线和圆相离,AB与圆O相离，d>r。（d为圆心到直线的距离）

  • 直线与圆的三种位置关系的判定与性质：
    （1）数量法：通过比较圆心O到直线距离d与圆半径的大小关系来判定，
    如果⊙O的半径为r，圆心O到直线l的距离为d，则有：
    直线l与⊙O相交d<r；
    直线l与⊙O相切d=r；
    直线l与⊙O相离d>r；
    （2）公共点法：通过确定直线与圆的公共点个数来判定。
    直线l与⊙O相交d<r2个公共点；
    直线l与⊙O相切d=r有唯一公共点；
    直线l与⊙O相离d>r无公共点 。

    圆的切线的判定和性质   
    （1）切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。
    （2）切线的性质定理：圆的切线垂直于经过切点的半径。

    切线长：
    在经过圆外一点的圆的切线上，这点和切点之间的线段的长叫做这点到圆的切线长。
    切线长定理：
    从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

  • 直线与圆的位置关系判定方法:
    平面内，直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0的位置关系判断一般方法是：
    1.由Ax+By+C=0，可得y=（-C-Ax）/B，（其中B不等于0），代入x2+y2+Dx+Ey+F=0，即成为一个关于x的方程
    如果b2-4ac>0，则圆与直线有2交点，即圆与直线相交。
    如果b2-4ac=0，则圆与直线有1交点，即圆与直线相切。
    如果b2-4ac<0，则圆与直线有0交点，即圆与直线相离。

    2.如果B=0即直线为Ax+C=0，即x=-C/A，它平行于y轴（或垂直于x轴），将x2+y2+Dx+Ey+F=0化为（x-a）2+（y-b）2=r2。
    令y=b，求出此时的两个x值x1、x2，并且规定x1<x2，那么： 
    当x=-C/A<x1或x=-C/A>x2时，直线与圆相离；
    当x1<x=-C/A<x2时，直线与圆相交。 
http://www.00-edu.com/ks/shuxue/2/159/2020-01-14/1969433.html十二生肖
十二星座