已知：三角形ABC中，∠A=90°，AB=AC，D为BC的中点（1）如图，E，F分别是AB，AC上的点，且BE=AF，求证：△DEF为等腰直角三角形。（2）若E，F分别为AB，CA延长线上的点，仍有BE=AF，其-九年级数学打印页面

已知：三角形ABC中，∠A=90°，AB=AC，D为BC的中点（1）如图，E，F分别是AB，AC上的点，且BE=AF，求证：△DEF为等腰直角三角形。（2）若E，F分别为AB，CA延长线上的点，仍有BE=AF，其-九年级数学

[db:作者] 2020-05-20 00:00:00 互联网

题文

已知：三角形ABC中，∠A=90°，AB=AC，D为BC的中点

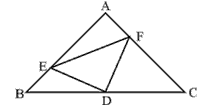（1）如图，E，F分别是AB，AC上的点，且BE=AF，求证：△DEF为等腰直角三角形。
（2）若E，F分别为AB，CA延长线上的点，仍有BE=AF，其他条件不变，那么，△DEF是否仍为等腰直角三角形？证明你的结论。
题型：证明题难度：中档

答案

（1）连结AD，因为AB=AC，∠BAC=90°D为BC的中点
         所以AD⊥BC ，BD=AD，所以∠B=∠DAC=45°
        又BE=AF，所以△BDE≌△ADF
        所以ED=FD，∠BDE=∠ADF
        所以∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°
        所以△DEF为等腰直角三角形
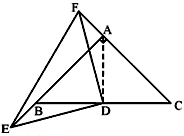
（2）若E，F分别是AB，CA延长线上的点，如图所示
         连结AD，因为AB=AC，∠BAC=90°，D为BC的中点
         所以AD=BD，AD⊥BC，所以∠DAC=∠ABD=45°
         所以∠DAF=∠DBE=135°
         又AF=BE，所以△DAF≌△DBE
         所以FD=ED，∠FDA=∠EDB
         所以∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°
         所以△DEF仍为等腰直角三角

据专家权威分析，试题“已知：三角形ABC中，∠A=90°，AB=AC，D为BC的中点（1）如图，E，F分别..”主要考查你对直角三角形的性质及判定，等腰三角形的性质，等腰三角形的判定等考点的理解。关于这些考点的“档案”如下：

直角三角形的性质及判定等腰三角形的性质，等腰三角形的判定

考点名称：直角三角形的性质及判定

直角三角形定义：
有一个角为90°的三角形，叫做直角三角形。直角三角形可用Rt△表示，如直角三角形ABC写作Rt△ABC。
直角三角形性质：
直角三角形是一种特殊的三角形，它除了具有一般三角形的性质外，具有一些特殊的性质：
性质1:直角三角形两直角边a，b的平方和等于斜边c的平方。即。如图，∠BAC=90°，则AB2+AC2=BC2（勾股定理)
性质2:在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°
性质3：在直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。
性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
性质5:

如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：
（1）（AD)2=BD·DC。
（2）（AB)2=BD·BC。
（3）（AC)2=CD·BC。
性质6:在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。
在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°。
性质7:如图，1/AB2+1/AC2=1/AD2
性质8:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
性质9：直角三角形直角上的角平分线与斜边的交点D 则 BD:DC=AB:AC
直角三角形的判定方法：
判定1：定义，有一个角为90°的三角形是直角三角形。
判定2：判定定理：以a、b、c为边的三角形是以c为斜边的直角三角形。如果三角形的三边a，b，c满足，那么这个三角形就是直角三角形。（勾股定理的逆定理）。
判定3：若一个三角形30°内角所对的边是某一边的一半，则这个三角形是以这条长边为斜边的直角三角形。
判定4：两个锐角互为余角（两角相加等于90°）的三角形是直角三角形。
判定5：若两直线相交且它们的斜率之积互为负倒数，则两直线互相垂直。那么
判定6：若在一个三角形中一边上的中线等于其所在边的一半，那么这个三角形为直角三角形。
判定7：一个三角形30°角所对的边等于这个三角形斜边的一半，则这个三角形为直角三角形。（与判定3不同，此定理用于已知斜边的三角形。）

考点名称：等腰三角形的性质，等腰三角形的判定

定义：
有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。
等腰三角形的性质：
1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)
等腰三角形的判定：
1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。

http://www.00-edu.com/ks/shuxue/2/160/2020-05-20/1991704.html十二生肖
十二星座