题文
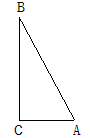
| 如图所示,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径作圆,当r=2.4cm时,AB与圆有怎样的位置关系?为什么? |
|
|
题型:解答题 难度:中档
答案
|
解:过C作CD⊥AB,垂足为D,在Rt△ABC中,AB= , 根据三角形的面积公式有CD·AB=AC·BC,∴CD= , 根据三角形的面积公式有CD·AB=AC·BC,∴CD= 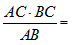 2.4cm, 2.4cm,
∵r=2.4cm,
∴r=CD,因此AB与⊙O相切。 |
据专家权威分析,试题“如图所示,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为..”主要考查你对 直角三角形的性质及判定,直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离) 等考点的理解。关于这些考点的“档案”如下:
直角三角形的性质及判定直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)
考点名称:直角三角形的性质及判定
考点名称:直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)

