|
题文
| 如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM上的一个动点(不与点B重合),连结AD,作BE⊥AD,垂足为E,连结CE,过点E作EF⊥CE,交BD于F. |
 |
(1)求证:BF=FD;
(2)∠A在什么范围内变化时,四边形ACFE是梯形,并说明理由;
(3)∠A在什么范围内变化时,线段DE上存在点G,满足条件DG=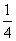 DA,并说明理由. DA,并说明理由. |
题型:解答题 难度:中档
答案
(1)在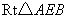 中 中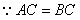 , ,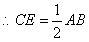 , , , ,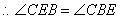 , ,
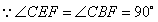  
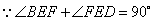 
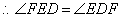  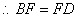
(2)由(1)BF=FD,而BC=CA,
 即 即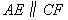

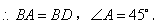
 ; ;
(3)
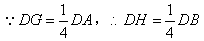
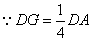 
又F为BD中点,H为DF的中点.
GH为DF的中垂线


 
又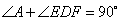 
 |
据专家权威分析,试题“如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM上的一个动点..”主要考查你对 直角三角形的性质及判定,梯形,梯形的中位线,平行线分线段成比例 等考点的理解。关于这些考点的“档案”如下:
直角三角形的性质及判定梯形,梯形的中位线平行线分线段成比例
考点名称:直角三角形的性质及判定 考点名称:梯形,梯形的中位线 考点名称:平行线分线段成比例
|

