|
题文
| 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5。点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动。伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E。点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止。设点P、Q运动的时间是t秒(t>0), |
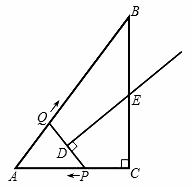 |
(1)当t=2时,AP=________,点Q到AC的距离是________;
(2)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)
(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值。若不能,请说明理由;
(4)当DE经过点C时,请直接写出t的值。 |
题型:解答题 难度:偏难
答案
解:(1)1;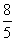 ; ;
(2)作QF⊥AC于点F,AQ=CP= t,
∴AP=3-t,
由△AQF∽△ABC,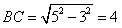 , ,
得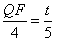 ,∴ ,∴ , ,
∴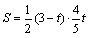 ,即 ,即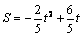 。 。 |
|
(3)能。
①当DE∥QB时,如图1,
∵DE⊥PQ,
∴PQ⊥QB,四边形QBED是直角梯形,
此时∠AQP=90°,
由△APQ∽△ABC,得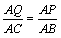 , ,
即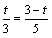 ,解得 ,解得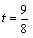 。 。
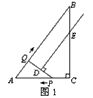
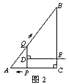
②如图2,当PQ∥BC时,DE⊥BC,
四边形QBED是直角梯形.此时∠APQ =90°,
由△AQP∽△ABC,得 , ,
即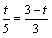 ,解得 ,解得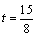 。 。 |
 |
(4) 或 或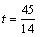 。 。 |
|
据专家权威分析,试题“如图,在Rt△ABC中,∠C=90°,AC=3,AB=5。点P从点C出发沿CA以每秒..”主要考查你对 直角三角形的性质及判定,求二次函数的解析式及二次函数的应用,勾股定理,梯形,梯形的中位线,相似三角形的性质 等考点的理解。关于这些考点的“档案”如下:
直角三角形的性质及判定求二次函数的解析式及二次函数的应用勾股定理梯形,梯形的中位线相似三角形的性质
考点名称:直角三角形的性质及判定 考点名称:求二次函数的解析式及二次函数的应用 考点名称:勾股定理 考点名称:梯形,梯形的中位线 考点名称:相似三角形的性质
|

