一副直角三角板即Rt△ABC和Rt△EDF如图1放置（其中△ABC为等腰直角三角形），E与A重合，D在AB上，DF经过点C，将△EDF绕点D逆时针方向旋转一个角度α至如图2所示。（1）求证：AE⊥BE；（2-九年级数学打印页面

一副直角三角板即Rt△ABC和Rt△EDF如图1放置（其中△ABC为等腰直角三角形），E与A重合，D在AB上，DF经过点C，将△EDF绕点D逆时针方向旋转一个角度α至如图2所示。（1）求证：AE⊥BE；（2-九年级数学

[db:作者] 2020-05-20 00:00:00 零零社区

题文

一副直角三角板即Rt△ABC和Rt△EDF如图1放置（其中△ABC为等腰直角三角形），E与A重合，D在AB上，DF经过点C，将△EDF绕点D逆时针方向旋转一个角度α至如图2所示。

（1）求证：AE⊥BE；
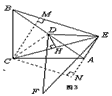
（2）如图3，连接CE，作DH⊥CE，则线段AE、BE与CH之间有何数量关系？写出关系式并加以证明；

（3）图3中若AB=4，当CH=____时，α=60°。（直接写出结果不用证明）
题型：解答题难度：偏难

答案

解：（1）△ABC为等腰直角三角形，CD⊥AB
∴AD=BD，
又AD与DE重合，
∴AD=BD=DE，
∴△ABC为直角三角形，∠AEB=90°，
即AE⊥BE；
（2）
证明如下：分别过C作CM⊥BE于M，CN⊥AE于N，
∵∠AEB=90°
∴四边形CMEN为矩形，
∴∠MCN=∠ACB=90°，
∴∠BCM=∠CAN 又AC=BC，
∴△BCM≌△CAN，
∴CM=CN，BM=AN
∴CE平分∠AEB，
∴∠CEB=∠CEA=45°
由CM=CN又得矩形CMEN为正方形，
∴EM=EN
∴AE+BE=EM+EN=2EM=

（3）。

据专家权威分析，试题“一副直角三角板即Rt△ABC和Rt△EDF如图1放置（其中△ABC为等腰直角三..”主要考查你对直角三角形的性质及判定，全等三角形的性质，矩形，矩形的性质，矩形的判定，图形旋转等考点的理解。关于这些考点的“档案”如下：

直角三角形的性质及判定全等三角形的性质矩形，矩形的性质，矩形的判定图形旋转

考点名称：直角三角形的性质及判定

直角三角形定义：
有一个角为90°的三角形，叫做直角三角形。直角三角形可用Rt△表示，如直角三角形ABC写作Rt△ABC。
直角三角形性质：
直角三角形是一种特殊的三角形，它除了具有一般三角形的性质外，具有一些特殊的性质：
性质1:直角三角形两直角边a，b的平方和等于斜边c的平方。即。如图，∠BAC=90°，则AB2+AC2=BC2（勾股定理)
性质2:在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°
性质3：在直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。
性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
性质5:

如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：
（1）（AD)2=BD·DC。
（2）（AB)2=BD·BC。
（3）（AC)2=CD·BC。
性质6:在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。
在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°。
性质7:如图，1/AB2+1/AC2=1/AD2
性质8:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
性质9：直角三角形直角上的角平分线与斜边的交点D 则 BD:DC=AB:AC
直角三角形的判定方法：
判定1：定义，有一个角为90°的三角形是直角三角形。
判定2：判定定理：以a、b、c为边的三角形是以c为斜边的直角三角形。如果三角形的三边a，b，c满足，那么这个三角形就是直角三角形。（勾股定理的逆定理）。
判定3：若一个三角形30°内角所对的边是某一边的一半，则这个三角形是以这条长边为斜边的直角三角形。
判定4：两个锐角互为余角（两角相加等于90°）的三角形是直角三角形。
判定5：若两直线相交且它们的斜率之积互为负倒数，则两直线互相垂直。那么
判定6：若在一个三角形中一边上的中线等于其所在边的一半，那么这个三角形为直角三角形。
判定7：一个三角形30°角所对的边等于这个三角形斜边的一半，则这个三角形为直角三角形。（与判定3不同，此定理用于已知斜边的三角形。）

考点名称：全等三角形的性质

全等三角形：
两个全等的三角形，而该两个三角形的三条边及三个角都对应地相等。全等三角形是几何中全等的一种。根据全等转换，两个全等三角形可以是平移、旋转、轴对称，或重叠等。当两个三角形的对应边及角都完全相对时，该两个三角形就是全等三角形。正常来说，验证两个全等三角形时都以三个相等部分来验证，最后便能得出结果。
全等三角形的对应边相等，对应角相等。
①全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边;
②全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角;
③有公共边的，公共边一定是对应边;
④有公共角的，角一定是对应角;
⑤有对顶角的，对顶角一定是对应角。
全等三角形的性质：
1.全等三角形的对应角相等。
2.全等三角形的对应边相等。
3.全等三角形的对应边上的高对应相等。
4.全等三角形的对应角的角平分线相等。
5.全等三角形的对应边上的中线相等。
6.全等三角形面积相等。
7.全等三角形周长相等。
8.全等三角形的对应角的三角函数值相等。

考点名称：矩形，矩形的性质，矩形的判定

矩形:
是一种平面图形，矩形的四个角都是直角，同时矩形的对角线相等，而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。
矩形的性质：
1．矩形的4个内角都是直角；
2．矩形的对角线相等且互相平分；
3．矩形所在平面内任一点到其两对角线端点的距离的平方和相等；
4．矩形既是轴对称图形，也是中心对称图形（对称轴是任何一组对边中点的连线），它至少有两条对称轴。对称中心是对角线的交点。
5．矩形是特殊的平行四边形，矩形具有平行四边形的所有性质
6.顺次连接矩形各边中点得到的四边形是菱形
矩形的判定：
①定义：有一个角是直角的平行四边形是矩形
②定理1：有三个角是直角的四边形是矩形
③定理2：对角线相等的平行四边形是矩形
④对角线互相平分且相等的四边形是矩形
矩形的面积：S_矩形=长×宽=ab。
黄金矩形:
宽与长的比是（√5-1）/2（约为0.618）的矩形叫做黄金矩形。
黄金矩形给我们一协调、匀称的美感。世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计。如希腊的巴特农神庙等。

考点名称：图形旋转

定义：
在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转。这个定点叫做旋转中心，转动的角度叫做旋转角。
图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变。
图形旋转性质：
（1）对应点到旋转中心的距离相等。
（2）对应点与旋转中心所连线段的夹角等于旋转角。
旋转对称中心
把一个图形绕着一个点旋转一定的角度后，与原来的图形相吻合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角。（旋转角大于0°小于360°）

http://www.00-edu.com/ks/shuxue/2/160/2020-05-20/1992310.html十二生肖
十二星座