|
题文
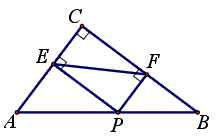
| 如图,已知在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P是斜边AB上(不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连结EF。随着P点在边AB上位置的改变,EF的长度是否也会改变?若不变,请你求EF的长度;若有变化,请你求EF的变化范围。 |
|
|
题型:解答题 难度:中档
答案
解:EF的长度会改变;
理由是:连接PC,
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=90°,
∵∠ACB=90°,
∴四边形PECF是矩形,
∴EF=PC,
∵AC=3,BC=4,
∴AB=5,
过点C作CD⊥AB,此时CD=PC且PC最小,
∴PC=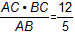 =2.4, =2.4,
∵点P是斜边AB上(不与A、B重合),
∴PC<BC=4,
∴PC的范围是2.4≤PC<4,
即EF的范围是2.4≤EF<4。 |
 |
据专家权威分析,试题“如图,已知在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P是斜边AB上(不..”主要考查你对 直角三角形的性质及判定,矩形,矩形的性质,矩形的判定 等考点的理解。关于这些考点的“档案”如下:
直角三角形的性质及判定矩形,矩形的性质,矩形的判定
考点名称:直角三角形的性质及判定 考点名称:矩形,矩形的性质,矩形的判定
|

