如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．（1）求证：PC是⊙O的切线；（2）求证：BC=12AB．-数学打印页面

如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．（1）求证：PC是⊙O的切线；（2）求证：BC=12AB．-数学

[db:作者] 2020-05-20 00:00:00 互联网

题文

如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．
（1）求证：PC是⊙O的切线；
（2）求证：BC=
1
2
AB．
题型：解答题难度：中档

答案

证明：（1）∵OA=OC，
∴∠A=∠OCA．
又∵∠COB为△AOC的外角，
∴∠COB=2∠OCA，又∠COB=2∠PCB，
∴∠OCA=∠PCB，
∵AB是⊙O直径，
∴∠ACB=90°，
∴∠OCA+∠OCB=90°，
∴∠PCB+∠OCB=90°，
∴∠PCO=90°，
∵点C在⊙O上，
∴PC是⊙O的切线；

（2）∵AB是⊙O的直径，
∴∠ACB=90°．
又∵点O是斜边AB的中点，
∴OC=
1
2
AB．
∵AC=PC，
∴∠A=∠P．
又由（1）知，∠OCA=∠PCB，
∴∠COB=∠OBC，
∴OC=BC=
1
2
AB，即BC=
1
2
AB．

据专家权威分析，试题“如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交..”主要考查你对直角三角形的性质及判定，圆心角，圆周角，弧和弦，直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）等考点的理解。关于这些考点的“档案”如下：

直角三角形的性质及判定圆心角，圆周角，弧和弦直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）

考点名称：直角三角形的性质及判定

直角三角形定义：
有一个角为90°的三角形，叫做直角三角形。直角三角形可用Rt△表示，如直角三角形ABC写作Rt△ABC。
直角三角形性质：
直角三角形是一种特殊的三角形，它除了具有一般三角形的性质外，具有一些特殊的性质：
性质1:直角三角形两直角边a，b的平方和等于斜边c的平方。即。如图，∠BAC=90°，则AB2+AC2=BC2（勾股定理)
性质2:在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°
性质3：在直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。
性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
性质5:

如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：
（1）（AD)2=BD·DC。
（2）（AB)2=BD·BC。
（3）（AC)2=CD·BC。
性质6:在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。
在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°。
性质7:如图，1/AB2+1/AC2=1/AD2
性质8:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
性质9：直角三角形直角上的角平分线与斜边的交点D 则 BD:DC=AB:AC
直角三角形的判定方法：
判定1：定义，有一个角为90°的三角形是直角三角形。
判定2：判定定理：以a、b、c为边的三角形是以c为斜边的直角三角形。如果三角形的三边a，b，c满足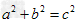，那么这个三角形就是直角三角形。（勾股定理的逆定理）。
判定3：若一个三角形30°内角所对的边是某一边的一半，则这个三角形是以这条长边为斜边的直角三角形。
判定4：两个锐角互为余角（两角相加等于90°）的三角形是直角三角形。
判定5：若两直线相交且它们的斜率之积互为负倒数，则两直线互相垂直。那么
判定6：若在一个三角形中一边上的中线等于其所在边的一半，那么这个三角形为直角三角形。
判定7：一个三角形30°角所对的边等于这个三角形斜边的一半，则这个三角形为直角三角形。（与判定3不同，此定理用于已知斜边的三角形。）

考点名称：圆心角，圆周角，弧和弦

圆的定义:
在同一平面内，到定点的距离等于定长的点的集合叫做圆。这个定点叫做圆的圆心。图形一周的长度，就是圆的周长。

弧：
圆上任意两点间的部分叫做圆弧，简称弧。
弧用符号“⌒”表示以A，B为端点的弧记作“”，读作“圆弧AB”或“弧AB”。
优弧：大于半圆的弧（多用三个字母表示）；
劣弧：小于半圆的弧（多用两个字母表示）
圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆。
弧、弦、弦心距、圆心角之间的关系定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等。
推论：在同圆或等圆中，如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。

圆心角：
顶点在圆心的角叫做圆心角。

圆周角：
顶点在圆上，并且两边都和圆相交的角叫做圆周角。
圆周角的顶点在圆上，它的两边为圆的两条弦。
圆心角特征识别:
①顶点是圆心；
②两条边都与圆周相交。

计算公式:
①L(弧长)=n/180Xπr（n为圆心角度数，以下同）；
②S(扇形面积) = n/360Xπr²；
③扇形圆心角n=（180L）/（πr）（度）。
④K=2Rsin(n/2) K=弦长；n=弦所对的圆心角，以度计。

圆心角定理:
圆心角的度数等于它所对的弧的度数。
理解：(定义）
（1）等弧对等圆心角
（2）把顶点在圆心的周角等分成360份时，每一份的圆心角是1°的角．
（3）因为在同圆中相等的圆心角所对的弧相等，所以整个圆也被等分成360份，这时，把每一份这样得到的弧叫做1°的弧．
（4）圆心角的度数和它们对的弧的度数相等．
推论：
在同圆或等圆中,如果(1)两个圆心角,(2)两条弧,(3)两条弦(4)两条弦上的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等

与圆周角关系:
在同圆或等圆中,同弧或同弦所对的圆周角等于二分之一的圆心角。
定理证明：分三种情况讨论，始终做直径COD，利用等腰三角形等腰底角相等，外角等于两内角之和来证明。

圆周角定理推论：
圆周角定理:在同圆或等圆中，同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。
①圆周角度数定理：圆周角的度数等于它所对的弧的度数的一半。
②同圆或等圆中，圆周角等于它所对的弧上的圆心角的一半。
③同圆或等圆中，同弧或等弧所对的圆周角相等，相等圆周角所对的弧也相等。（不在同圆或等圆中其实也相等的。注：仅限这一条。）
④半圆（或直径）所对圆周角是直角，90°的圆周角所对的弦是直径。
⑤圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。
⑥在同圆或等圆中，圆周角相等<=>弧相等<=>弦相等。

考点名称：直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）

直线与圆的位置关系:
直线与圆的位置关系有三种：直线与圆相交，直线与圆相切，直线与圆相离。
（1）相交：直线和圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线，公共点叫做交点AB与⊙O相交，d<r；
（2）相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线，这个唯一的公共点叫做切点。AB与⊙O相切，d=r。
（3）相离：直线和圆没有公共点时，叫做直线和圆相离,AB与圆O相离，d>r。（d为圆心到直线的距离）
直线与圆的三种位置关系的判定与性质：
（1）数量法：通过比较圆心O到直线距离d与圆半径的大小关系来判定，
如果⊙O的半径为r，圆心O到直线l的距离为d，则有：
直线l与⊙O相交d<r；
直线l与⊙O相切d=r；
直线l与⊙O相离d>r；
（2）公共点法：通过确定直线与圆的公共点个数来判定。
直线l与⊙O相交d<r2个公共点；
直线l与⊙O相切d=r有唯一公共点；
直线l与⊙O相离d>r无公共点。

圆的切线的判定和性质
（1）切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。
（2）切线的性质定理：圆的切线垂直于经过切点的半径。

切线长：
在经过圆外一点的圆的切线上，这点和切点之间的线段的长叫做这点到圆的切线长。
切线长定理：
从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。
直线与圆的位置关系判定方法:
平面内，直线Ax+By+C=0与圆x²+y²+Dx+Ey+F=0的位置关系判断一般方法是：
1.由Ax+By+C=0，可得y=（-C-Ax）/B，（其中B不等于0），代入x²+y²+Dx+Ey+F=0，即成为一个关于x的方程
如果b²-4ac>0，则圆与直线有2交点，即圆与直线相交。
如果b²-4ac=0，则圆与直线有1交点，即圆与直线相切。
如果b²-4ac<0，则圆与直线有0交点，即圆与直线相离。

2.如果B=0即直线为Ax+C=0，即x=-C/A，它平行于y轴（或垂直于x轴），将x²+y²+Dx+Ey+F=0化为（x-a）²+（y-b）²=r²。
令y=b，求出此时的两个x值x₁、x₂，并且规定x₁<x₂，那么：
当x=-C/A<x₁或x=-C/A>x₂时，直线与圆相离；
当x^₁<x=-C/A<x₂时，直线与圆相交。

http://www.00-edu.com/ks/shuxue/2/160/2020-05-20/1994719.html十二生肖
十二星座