|
题文
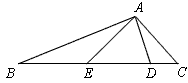
如图,在△ABC 中,∠C=2∠B ,D是BC边上一点,且AD⊥AB,点E 是线段BD的中点,连结AE
(1)求证:BD=2AC ;
(2)若AC2=DC·BC ,求证:△AEC是等腰直角三角形。 |
 |
题型:证明题 难度:偏难
答案
证明:(1)∵ ∴ ∴
∵点E是BD的中点,∴ 即 即
∴ ∴ ∴
∵ ∴ ∴
又∵ ∴ ∴ ∴ ∴
∵ ∴ ∴
(2)∵ ∴ ∴
又∵ ∴ ∴ ∽ ∽ ∴ ∴
又∵ ∴ ∴
∵ ∴ ∴ 即 即
又 所以 所以 是等腰直角三角形。 是等腰直角三角形。 |
据专家权威分析,试题“如图,在△ABC中,∠C=2∠B,D是BC边上一点,且AD⊥AB,点E是线段BD的..”主要考查你对 等腰三角形的性质,等腰三角形的判定,直角三角形的性质及判定 等考点的理解。关于这些考点的“档案”如下:
等腰三角形的性质,等腰三角形的判定直角三角形的性质及判定
考点名称:等腰三角形的性质,等腰三角形的判定 考点名称:直角三角形的性质及判定
|

