|
题文
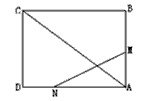
| 如图,已知矩形ABCD的边长AB=3cm,BC=6cm,某一时刻,动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动;同时,动点N从点D沿DA方向以2cm/s的速度向点A匀速运动。 |
|
|
(1)经过多少时间,△AMN的面积等于矩形ABCD面积的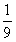 ? ?
(2)是否存在时刻t,使A、M、N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由。 |
题型:解答题 难度:中档
答案
解:(1)设经过x秒,△AMN的面积等于矩形ABCD面积的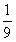 , ,
由题意得DN=2x,AN=6-2x, AM=x,
∵矩形ABCD中AB=3,BC=6,
∴AD=BC=6,CD=AB=3,
从而矩形ABCD的面积为AB·AD=3×6=18,
△AMN的面积= , ,
可得方程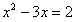 , ,
解得: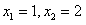 , ,
所以,经过1秒或2秒,△AMN的面积等于矩形ABCD面积的 ; ;
(2)由题意得DN=2t,AN=6-2t,AM=t,
若 , ,
则有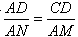 ,即 ,即 , ,
解得:x=1.5;
若 , ,
则有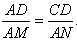 ,即 ,即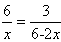 , ,
解得:x=2.4,
所以,当t=1.5秒或2.4秒时,以A、M、N为顶点的三角形与△ACD相似。 |
据专家权威分析,试题“如图,已知矩形ABCD的边长AB=3cm,BC=6cm,某一时刻,动点M从点A..”主要考查你对 三角形的周长和面积,矩形,矩形的性质,矩形的判定,相似三角形的性质 等考点的理解。关于这些考点的“档案”如下:
三角形的周长和面积矩形,矩形的性质,矩形的判定相似三角形的性质
考点名称:三角形的周长和面积 考点名称:矩形,矩形的性质,矩形的判定 考点名称:相似三角形的性质
|

