|
解:(2)图2中结论PR+PQ=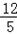 仍成立. 仍成立.
证明:连接BP,过C点作CK?BD于点K.
∵四边形ABCD为矩形, ∴∠BCD=90°,
又∵CD=AB=3,BC=4, ∴BD= = = =5. ∵S△BCD= =5. ∵S△BCD= BC×CD= BC×CD= BD×CK, BD×CK,
∴3×4=5CK,
∴CK= . .
∵S△BCE= BE×CK,S△BEP= BE×CK,S△BEP= PR×BE, S△BCP= PR×BE, S△BCP= PQ×BC,且S△BCE=S△BEP+S△BCP, PQ×BC,且S△BCE=S△BEP+S△BCP,
∴ BE×CK= BE×CK= PR×BE+ PR×BE+ PQ×BC, PQ×BC,
又∵BE=BC,
∴ CK= CK= PR+ PR+ PQ, PQ,
∴CK=PR+PQ,
又∵CK= , ,
∴PR+PQ=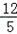 ; ;
(3)连接BP,S△BPE﹣S△BCP=S△BEC,
S△BEC 是固定值,
BE=BC 为两个底,
PR,PQ 分别为高,
图3中的结论是PR﹣PQ=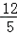 . .
|

