零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 三角形的周长和面积 > 正文 返回　打印

对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB、BC、CA至点A1、B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1；第二次-数学
[db:作者]  2020-05-20 00:00:00  互联网

题文

对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB、BC、CA至点A1、B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1；第二次操作，分别延长A1B1、B1C1、C1A1至点A2、B2、C2，使得A2B1=2A1B1，B2C1=2B1C1，C2A1=2C1A1，顺次连接A2、B2、C2，得到△A2B2C2，记其面积为S2；…；按此规律继续下去，可得到△AnBnCn．
（1）求面积S1；（2）求面积Sn．

题型：解答题  难度：中档

答案



连BC1，
∵C1A=2CA，
∴S△ABC1=2S△ABC，
同理：S△A1BC1=2S△ABC1=4S△ABC，
∴S△A1AC1=6S△ABC，
同理：S△A1BB1=S△CB1C1=6S△ABC，
∴S△A1B1C1=19S△ABC，
即S1=19S0，
∵S0=S△ABC=1，
∴S1=19；

（2）同理，S2=19S1=192S0，S3=193S0，
∴Sn=19nS0=19n．

据专家权威分析，试题“对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB、BC、..”主要考查你对  三角形的周长和面积  等考点的理解。关于这些考点的“档案”如下：

三角形的周长和面积

考点名称：三角形的周长和面积

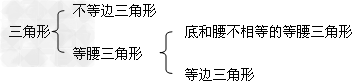  • 三角形的概念：
    由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

    构成三角形的元素：
    边：组成三角形的线段叫做三角形的边；
    顶点：相邻两边的公共端点叫做三角形的顶点；
    内角：相邻两边所组成的角叫做三角形的内角，简称三角形的角。

    三角形有下面三个特性：
    （1）三角形有三条线段；
    （2）三条线段不在同一直线上；
    （3）首尾顺次相接。

    三角形的表示：
    用符号“△，顶点是A、B、C的三角形记作“△ABC”，读作ABC”。

  • 三角形的分类：
    （1）三角形按边的关系分类如下：
    ；
    （2）三角形按角的关系分类如下：

    把边和角联系在一起，我们又有一种特殊的三角形：等腰直角三角形。它是两条直角边相等的直角三角形。

  • 三角形的周长和面积：
    三角形的周长等于三角形三边之和。
    三角形面积=（底×高）÷2。
http://www.00-edu.com/ks/shuxue/2/163/2020-05-20/1992078.html十二生肖
十二星座