 |
首页 > 考试 > 数学 > 初中数学 > 三角形的周长和面积 > 正文 | 返回 打印 |
|
 |
首页 > 考试 > 数学 > 初中数学 > 三角形的周长和面积 > 正文 | 返回 打印 |
|
答案
| (1)S1=24,S2=24,S3=24; (2)对于线段AC与线段BD垂直相交(垂足O不与点A,C,B,D重合)的任意情形,四边形ABCD的面积为定值24. 证明如下: ∵AC⊥BD, ∴S△BAC=
∴S四边形ABCD=
(3)顺次连接点A,B,C,D,A所围成的封闭图形的面积仍为24. 证明:∵AC⊥BD, ∴S△ABD=
∴S四边形ABCD=S△ABD+S△BCD=
|
据专家权威分析,试题“已知线段AC=8,BD=6.(1)已知线段AC垂直于线段BD.设图1,图2和图3..”主要考查你对 三角形的周长和面积,多边形 等考点的理解。关于这些考点的“档案”如下:
三角形的周长和面积多边形
考点名称:三角形的周长和面积
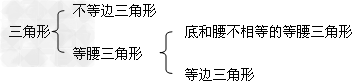 ;
;
考点名称:多边形
多边形定理:
1、内角和定理:
n边形的内角和等于(n-2)x180°
可逆用:
·n边形的边=(内角和÷180°)+2
·过n边形一个顶点有(n-3)条对角线
·因为每个顶点和它自己及相邻的两个顶点都不能做对角线,所以n边形的每个顶点只能和n-3个其他的顶点之间做对角线,又因为每一条对角线都要连结两个顶点,所以要除以2。
n边形共有n×(n-3)÷2个对角线
· n边形过一个顶点引出所有对角线后,把多边形分成n-2个三角形
推论:
·任意凸形多边形的外角和都等于360°。
·多边形对角线的计算公式:n边形的对角线条数等于1/2·n(n-3)
·在平面内,各边相等,各内角也都相等的多边形叫做正多边形。【两个条件必须同时满足
反例:矩形(各内角相等,各边不一定相等);菱形(各边相等,各内角不一定相等)】
2、外角和定理:
n边形外角和等于n·180°-(n-2)·180°=360°
多边形的每个内角与它相邻的外角是邻补角,所以n边形内角和加外角和等于n·180°