如图，在菱形ABCD中，E，F分别是AB，AC的中点，如果EF=2，那么菱形的周长为______．-数学打印页面

如图，在菱形ABCD中，E，F分别是AB，AC的中点，如果EF=2，那么菱形的周长为______．-数学

[db:作者] 2020-05-22 00:00:00 零零社区

题文

如图，在菱形ABCD中，E，F分别是AB，AC的中点，如果EF=2，那么菱形的周长为______．
题型：填空题难度：中档

答案

∵菱形ABCD中，E，F分别是AB，AC的中点，EF=2，
∴BC=2EF=2×2=4．即AB=BC=CD=AD=4．故菱形的周长为4BC=4×4=16．
故答案为16．

据专家权威分析，试题“如图，在菱形ABCD中，E，F分别是AB，AC的中点，如果EF=2，那么菱..”主要考查你对三角形中位线定理，菱形，菱形的性质，菱形的判定等考点的理解。关于这些考点的“档案”如下：

三角形中位线定理菱形，菱形的性质，菱形的判定

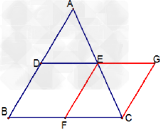
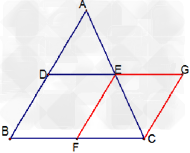
考点名称：三角形中位线定理

三角形中位线定义：
连接三角形两边中点的线段叫做三角形的中位线。一个三角形共有三条中位线。
三角形中位线定理：
三角形的中位线平行于第三边，并且等于它的一半。

如图已知△ABC中，D，E分别是AB，AC两边中点。
则DE平行于BC且等于BC/2
三角形中位线逆定理：

逆定理一：在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线。
如图DE//BC，DE=BC/2，则D是AB的中点，E是AC的中点。
逆定理二：在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线。
如图D是AB的中点，DE//BC，则E是AC的中点，DE=BC/2
区分三角形的中位线和中线：
三角形的中位线是连结三角形两边中点的线段；
三角形的中线是连结一个顶点和它的对边中点的线段。

考点名称：菱形，菱形的性质，菱形的判定

菱形的定义:
在一个平面内，有一组邻边相等的平行四边形是菱形。
菱形的性质:
①菱形具有平行四边形的一切性质；
②菱形的对角线互相垂直且平分，并且每一条对角线平分一组对角；
③菱形的四条边都相等；
④菱形既是轴对称图形（两条对称轴分别是其两条对角线所在的直线），也是中心对称图形（对称中心是其重心，即两对角线的交点）；
⑤在有一个角是60°角的菱形中，较短的对角线等于边长，较长的对角线是较短的对角线的根号3倍。
菱形的判定:
在同一平面内，
（1）定义：有一组邻边相等的平行四边形是菱形
（2）定理1：四边都相等的四边形是菱形
（3）定理2：对角线互相垂直的平行四边形是菱形
菱形是在平行四边形的前提下定义的，首先它是平行四边形，而且是特殊的平行四边形，特殊之处就是“有一组邻边相等”，因而增加了一些特殊的性质和判定方法。
菱形的面积：S_菱形=底边长×高=两条对角线乘积的一半。

http://www.00-edu.com/ks/shuxue/2/165/2020-05-22/2000716.html十二生肖
十二星座