已知点A、B到直线l的距离分别为4与6，E是线段AB的中点，那么点E到直线l的距离是______．-数学打印页面

已知点A、B到直线l的距离分别为4与6，E是线段AB的中点，那么点E到直线l的距离是______．-数学

[db:作者] 2020-05-22 00:00:00 互联网

题文

已知点A、B到直线l的距离分别为4与6，E是线段AB的中点，那么点E到直线l的距离是______．
题型：填空题难度：中档

答案

如图一
AD⊥l于D，BC⊥l于C，且AD=4，BC=6，E是AB的中点，EF⊥l于F，求EF．
∵AD⊥l于D，BC⊥l，EF⊥l于F，
∴AD∥EF∥BC，
∴ABCD是直角梯形，
∵AE=BE，
∴DF=CF，
∴EF=（AD+BC）÷2=（4+6）÷2=5．

如图二
AD⊥l于D，BC⊥l于C，且AD=4，BC=6，E是AB的中点，EF⊥l于F，求EF．
∵AD⊥l于D，BC⊥l，EF⊥l于F，
∴AD∥EF∥BC，
∴△EOF∽△AOD∽△BOC，
∵AD=4，BC=6，E是AB的中点，
∴AD：BC=2：3，EF：AD=1：4，
∴EF=1．
故答案为5或1．

据专家权威分析，试题“已知点A、B到直线l的距离分别为4与6，E是线段AB的中点，那么点E到..”主要考查你对三角形中位线定理，梯形，梯形的中位线等考点的理解。关于这些考点的“档案”如下：

三角形中位线定理梯形，梯形的中位线

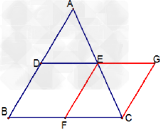
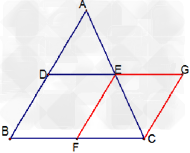
考点名称：三角形中位线定理

三角形中位线定义：
连接三角形两边中点的线段叫做三角形的中位线。一个三角形共有三条中位线。
三角形中位线定理：
三角形的中位线平行于第三边，并且等于它的一半。

如图已知△ABC中，D，E分别是AB，AC两边中点。
则DE平行于BC且等于BC/2
三角形中位线逆定理：

逆定理一：在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线。
如图DE//BC，DE=BC/2，则D是AB的中点，E是AC的中点。
逆定理二：在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线。
如图D是AB的中点，DE//BC，则E是AC的中点，DE=BC/2
区分三角形的中位线和中线：
三角形的中位线是连结三角形两边中点的线段；
三角形的中线是连结一个顶点和它的对边中点的线段。

考点名称：梯形，梯形的中位线

梯形的定义：
一组对边平行，另一组对边不平行的四边形叫做梯形。
梯形中平行的两边叫做梯形的底，通常把较短的底叫做上底，较长的底叫做下底，梯形中不平行的两边叫做梯形的腰，梯形的两底的距离叫做梯形的高。
梯形的中位线：
连结梯形两腰的中点的线段。
梯形性质：
①梯形的上下两底平行；
②梯形的中位线（两腰中点相连的线叫做中位线）平行于两底并且等于上下底和的一半。
③等腰梯形对角线相等。

梯形判定：
1.一组对边平行，另一组对边不平行的四边形是梯形。
2.一组对边平行且不相等的四边形是梯形。

梯形中位线定理：
梯形中位线平行于两底，并且等于两底和的一半。
梯形中位线×高=（上底+下底）×高=梯形面积
梯形中位线到上下底的距离相等
中位线长度=（上底+下底）

梯形的周长与面积：
梯形的周长公式：上底+下底+腰+腰，用字母表示：a+b+c+d。
等腰梯形的周长公式：上底+下底+2腰，用字母表示：a+b+2c。
梯形的面积公式：（上底+下底）×高÷2，用字母表示：S=（a+b）×h。
变形1：h=2s÷（a+b）；
变形2：a=2s÷h-b；
变形3：b=2s÷h-a。
另一计算梯形的面积公式：中位线×高，用字母表示：L·h。
对角线互相垂直的梯形面积为：对角线×对角线÷2。
梯形的分类：

等腰梯形：两腰相等的梯形。
直角梯形：有一个角是直角的梯形。

等腰梯形的性质：
（1）等腰梯形的同一底边上的两个角相等。
（2）等腰梯形的对角线相等。
（3）等腰梯形是轴对称图形。

等腰梯形的判定：
（1）定义：两腰相等的梯形是等腰梯形
（2）定理：在同一底上的两个角相等的梯形是等腰梯形
（3）对角线相等的梯形是等腰梯形。

http://www.00-edu.com/ks/shuxue/2/165/2020-05-22/2001020.html十二生肖
十二星座