零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 三角形中位线定理 > 正文 返回　打印

如图，已知E，F，G，H是四边形ABCD各边的中点，则S四边形EFGH：S四边形ABCD的值是______．-数学
[db:作者]  2020-05-22 00:00:00  互联网

题文

如图，已知E，F，G，H是四边形ABCD各边的中点，则S四边形EFGH：S四边形ABCD的值是______．

题型：填空题  难度：偏易

答案



连接AC，BD．
因为G、F为CD、BC边中点，所以GF=
1
2
DB．
由于△CGF∽△CDB，所以
S△CGF=
1
4
S△CDB，
同理可得S△DHG=
1
4
S△CDA，S△HAE=
1
4
S△DAB，S△BEF=
1
4
S△CAB，于是
S△CGF+S△DHG+S△HAE+S△BEF=
1
4
（S△CDB+S△CDA+S△DAB+S△CAB）=
1
4
×2S四边形ABCD=
1
2
S四边形ABCD，
S四边形EFGH：S四边形ABCD=1：2

据专家权威分析，试题“如图，已知E，F，G，H是四边形ABCD各边的中点，则S四边形EFGH：S四..”主要考查你对  三角形中位线定理，相似多边形的性质  等考点的理解。关于这些考点的“档案”如下：

三角形中位线定理相似多边形的性质

考点名称：三角形中位线定理

  • 三角形中位线定义：
    连接三角形两边中点的线段叫做三角形的中位线。一个三角形共有三条中位线。
    三角形中位线定理：
    三角形的中位线平行于第三边，并且等于它的一半。

    如图已知△ABC中，D，E分别是AB，AC两边中点。
    则DE平行于BC且等于BC/2

  • 三角形中位线逆定理：

    逆定理一：在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线。
    如图DE//BC，DE=BC/2，则D是AB的中点，E是AC的中点。
    逆定理二：在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线。
    如图D是AB的中点，DE//BC，则E是AC的中点，DE=BC/2

  • 区分三角形的中位线和中线：
    三角形的中位线是连结三角形两边中点的线段；
    三角形的中线是连结一个顶点和它的对边中点的线段。

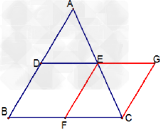
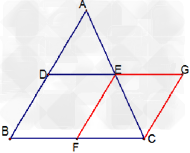
考点名称：相似多边形的性质

  • 相似多边形：
    如果两个边数相同的多边形的对应角相等，对应边成比例，这两个或多个多边形叫做相似多边形，相似多边形对应边的比叫做相似比。（或相似系数）
    判定:
    如果对应角相等,对应边成比例的多边形是相似多边形.
    如果所有对应边成比例，那么这两个多边形相似

  • 相似多边形的性质：
    相似多边形的性质定理1：相似多边形周长比等于相似比。
    相似多边形的性质定理2：相似多边形对应对角线的比等于相似比。
    相似多边形的性质定理3：相似多边形中的对应三角形相似，其相似比等于相似多边形的相似比。
    相似多边形的性质定理4：相似多边形面积的比等于相似比的平方。
    相似多边形的性质定理5：若相似比为1，则全等。
    相似多边形的性质定理6：相似三角形的对应线段（边、高、中线、角平分线）成比例。
    相似多边形的性质定理7：相似三角形的对应角相等，对应边成比例。
    相似多边形的性质定理主要根据它的定义：对应角相等，对应边成比例。
http://www.00-edu.com/ks/shuxue/2/165/2020-05-22/2001227.html十二生肖
十二星座