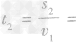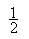汽车以10m/s的速度向前行驶,司机鸣笛后5s钟听到正前方山崖反射回来的声音,此时汽山距山崖有多远?-八年级物理
题文
| 汽车以10m/s的速度向前行驶,司机鸣笛后5s钟听到正前方山崖反射回来的声音,此时汽山距山崖有多远? |
答案
| 解:在t=5s的时间内,汽车行驶的距离: s1=v1t=10m/s×5s=50m, 声音传播的距离: s2=v2t=340m/s×5s=1700m, 设司机鸣笛时汽车到山崖的距离为s, 则:2s=s1+s2, ∴s=  = = =875m. =875m. |
据专家权威分析,试题“汽车以10m/s的速度向前行驶,司机鸣笛后5s钟听到正前方山崖反射回..”主要考查你对 回声及回声测距离的应用,速度公式及其应用 等考点的理解。关于这些考点的“档案”如下:
回声及回声测距离的应用速度公式及其应用
考点名称:回声及回声测距离的应用
- 定义:
声音在传播过程中遇到障碍物要发生反射,人们把声音遇到障碍物反射回来的声音叫回声 - 区别回声与原声:
回声的概念 回声是由于声音被高墙、山崖反射而产生的,对着远处的高墙、山崖呼喊能够听到回声 区分回声与原声的条件 若回声到达人耳比原声晚0.1s以上,人耳就能把回声和原声区分开来。在空气中,讲话人与反射物间距离必须在17m以上,否则,回声与原声混在一起,使原声加强 - 人耳辨别出回声的条件:
人耳辨别出回声的条件:也就是人耳区分两次声音的条件是:反射回来的声音到达人耳比原声晚0.1秒以上,否则原声和回声混合在一起使原声加强,这就是在屋里说话为什么比在旷野里说话听起来响的原因。
回声测距离的例题剖析:
例:汽车沿平直公路匀速使向一座高山,汽车的速度为10m/s,声速为340m/s,行进途中按一次喇叭,2s后司机听到回声,求司机按喇叭处距山脚距离是多少
剖析:发出声听到回声这段时间走的路程为s1=v1t,而汽车在这段时间走的路程为s2=v2t,
鸣笛处到山脚距离s=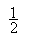 (s1+s2)=
(s1+s2)= (v1t+v2t)=
(v1t+v2t)=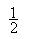 (10m/s+340m/s)×2s=350m,
(10m/s+340m/s)×2s=350m,
所以答案为:350m。 - 回声定位:
蝙蝠在飞行时会发出超声波,这些超声波碰到墙壁或昆虫时会反射回来,根据回声传来的方位和时间,蝙蝠可以确定目标的位置和距离。蝙蝠采用的这种方法叫做回声定位(如图所示)。
回声的应用:
利用回声可以测量距离,如:海底的深度、河宽以及回声定位
考点名称:速度公式及其应用
- 速度的公式:
 ,其中v表示速度,s表示路程,t表示时间。
,其中v表示速度,s表示路程,t表示时间。
注意:
①应用 计算时,单位要统一。s用米(m),t用秒(s)作单位时,速度v的单位为米/秒 (m/s);当s用千米(km),t用小时(h)时,速度v的单位为千米/时(km/h)。
计算时,单位要统一。s用米(m),t用秒(s)作单位时,速度v的单位为米/秒 (m/s);当s用千米(km),t用小时(h)时,速度v的单位为千米/时(km/h)。
②公式 的三个物理量必须对应于同一物体。
的三个物理量必须对应于同一物体。 火车过桥(隧道)问题:
火车穿过隧道时,火车头进人隧道就开始算起,直到火车尾离开隧道才叫做火车通过了隧道,所以火车穿过隧道经过的路程应该等于隧道长与车身长度的和。过大桥时也类似,火车通过大桥经过的路程等于桥长加车长。故对于本身有长度的物体过桥问题小结如下:物体通过的路程等于桥长与物体本身长度的和。例1:一列火车长200米,用20s的时间穿过了一条100m长的隧道,该火车如果以这样的速度通过长 3.4km的大桥,要用多长时间?
解析:火车穿过隧道时所走的路程:
 =100m+200m=300m,时间t1=20s,火车的速度:vl =
=100m+200m=300m,时间t1=20s,火车的速度:vl = ,此速度也是火车通过大桥的速度,火车通过大桥的路程:
,此速度也是火车通过大桥的速度,火车通过大桥的路程: =3400m+ 200m=3600m,通过此桥需要的时间为
=3400m+ 200m=3600m,通过此桥需要的时间为
 。
。
答案:240s出租车问题:
1.出租车的速度表示车辆行驶过程中的行进速度,指针指示的数值就是该时刻的速度值,采用的单位为km/h。
2.里程示数窗表示该车行驶的总路程,某段时间的路程就等于这段时间内两个示数的差。
3.出租车票据上给出的上车、下车时间间隔为车行驶时间,里程就是这段时间内出租车通过的路程。利用这些信息,可以解决与出租车有关的多种问题。例某人乘出租车时得到一张天津市客运出租行业专用发票,如表所示,此人乘车时间为____;该车这段时间内运动的平均速度为____km/h。

- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |