小妍站在一竖立的平面镜前,已知她到平面镜的距离为9米,现在她以1.5米/秒的速度朝镜面走去,求:(1)在未走动之前,小妍的像到镜面的距离是多少?小妍的像到小妍自身的距离是-物理
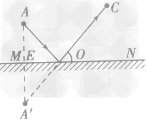
(2)连接A'C与MN交于0点,0点为入射点(DC 是反射光线)。
(3)连接AO,并在AO、OC上画出箭头表示光的传播方向,AO就是入射光线,OC是经平面镜反射通过眼睛的光线。
答案:如图所示
巧解平面镜的时钟问题
(1)逆向读法
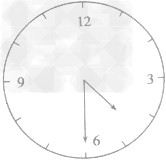
根据平面镜成像规律和成像性质,镜中“钟面”与实际钟面总是相对于平面镜对称。即实际时钟(如图甲所示)的指针按顺时针方向走动时,镜中“钟面”内表示钟点的数字是按上“12”、下“6”、左“3”和右“9”排列。如图乙所示的实际时刻为7:30。
(2)还原法
由平面镜成像的性质,镜叶1“钟面”与实际钟面左右对称。因此,镜中“钟面”的“背面”与实际钟面相对应.即还原出一个实际的钟面。这样,对印刷在书籍或试卷上的镜中“钟面”,只要从其背面对着光亮处透视 “钟面”并直接从中读取钟点数,即为实际钟点数?如图乙所示镜中“钟面”读得实际点数为7:30.
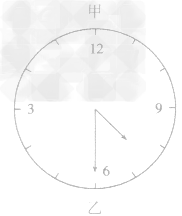
(3)对称作图法根据平面镜成像性质——像与物左右对称。.镜中 “钟面”内的“指针”位置与实际钟面内的指针位置对称。因此,求解这类“镜中时钟”问题,只要由镜中“钟面”作出以上“12”下“6”为对称轴的指针位置图形,再对作出的图形按实际钟面读出钟点数。图所示虚线为实线所示镜中“指针”的左右对称图形,读得实际钟点数为9:40。
等效替代法探究平面镜的成像特点
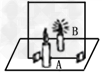
等效替代法就是在保证某一方面效果相同的前提下,用理想的、熟悉的、简单的物理对象、物理过程、物理现象替代实际的、陌生的、复杂的物理对象、物理过程、物理现象的思想方法。主要有:物理模型的等效替代,物理过程的等效替代,作用效果的等效替代以及物理图形的等效替代等形式例小红同学在做“探究平面镜成像”的实验时,将一块玻璃板竖直放存水平台上,再取两段完全相同的蜡烛。A和B,点燃玻璃板前的蜡烛A,进行观察,如图所示,在此实验中:
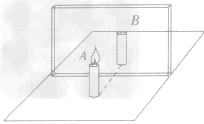
(1)小红选择玻璃板代替镜子进行实验的目的是______________。
(2)刻度K的作用是便于比较像与物________________。
__关系。
(3)选取两段完全相同的蜡烛是为了比较像与物的__关系。
(4)移走后面的蜡烛B,并在其所存位置上放一光屏,则光屏上____接收到蜡烛烛焰的像(选填 “能”或“不能”)。所以平面镜所成的像是____ (选填“实”或“虚”)像。
(5)小红将蜡烛A逐渐远离玻璃板时,它的像的大小(选填“变大”、“变小”或“不变”)。
(6)在玻璃板的同一侧,该同学通过玻璃看到了同一个蜡烛的两个像,产生这种现象的原因是_____。
解析:研究平面镜成像特点时,要研究像的大小、倒正及到平面镜的距离关系等,采用玻璃板的目的是利用了玻璃板能透光,在物A侧能观察到另一侧的情况,这样当A的像与另一侧B重合时,说明B所在位置就是A的像的位置,观察像与物的大小关系,并用刻度尺测出A、B分别到平面镜的距离,就可判断两距离大小和像的大小。当取走B,放上光屏时,在光屏上得不到像,而只能用眼睛存物一侧观察玻璃板才能看到,所以说平面镜所成的像是一个正立、等大的虚像,当物体逐渐远离平面镜时,像的大小不变。
答案:(1)能准确找到像的位置 (2)到平面镜的距离 (3)大小 (4)不能 虚 (5)不变 (6)玻璃的两个表面同时发生反射,各成一个像
同一物体靠近或远离平面镜时,像的大小变化问题
物体在平面镜中成的是正立的虚像,像与物体大小相等,即像的大小与物体的大小有关,与物体距平面镜的远近、平面镜的大小等因素无关。
例:某同学从远处走向一面穿衣镜,他住镜中像的大小及像和人之问的距离的变化情况正确的是 ( )
A.像大小不变,像和人之问的距离变小
B.像变大,像和人之间的距离变大
C.像变大,像和人之间的距离变小
D.像大小不变,像和人之间的距离不变
解析:像的大小与物体到平面镜的距离无关,我们平常说的所谓远小近大,只是人的视觉造成的错觉。根据平面镜成像特点可以知道,像和物大小相等,像和物到镜面的距离相等。因为该同学的大小没有变化,所以像大小小变;而该同学到平面镜的距离在变小,所以像到平面镜的距离也在变小,从而像和人之间的距离在变小。
答案:A
考点名称:速度公式及其应用
- 速度的公式:
 ,其中v表示速度,s表示路程,t表示时间。
,其中v表示速度,s表示路程,t表示时间。
注意:
①应用 计算时,单位要统一。s用米(m),t用秒(s)作单位时,速度v的单位为米/秒 (m/s);当s用千米(km),t用小时(h)时,速度v的单位为千米/时(km/h)。
计算时,单位要统一。s用米(m),t用秒(s)作单位时,速度v的单位为米/秒 (m/s);当s用千米(km),t用小时(h)时,速度v的单位为千米/时(km/h)。
②公式 的三个物理量必须对应于同一物体。
的三个物理量必须对应于同一物体。 火车过桥(隧道)问题:
火车穿过隧道时,火车头进人隧道就开始算起,直到火车尾离开隧道才叫做火车通过了隧道,所以火车穿过隧道经过的路程应该等于隧道长与车身长度的和。过大桥时也类似,火车通过大桥经过的路程等于桥长加车长。故对于本身有长度的物体过桥问题小结如下:物体通过的路程等于桥长与物体本身长度的和。例1:一列火车长200米,用20s的时间穿过了一条100m长的隧道,该火车如果以这样的速度通过长 3.4km的大桥,要用多长时间?
解析:火车穿过隧道时所走的路程:
 =100m+200m=300m,时间t1=20s,火车的速度:vl =
=100m+200m=300m,时间t1=20s,火车的速度:vl = ,此速度也是火车通过大桥的速度,火车通过大桥的路程:
,此速度也是火车通过大桥的速度,火车通过大桥的路程: =3400m+ 200m=3600m,通过此桥需要的时间为
=3400m+ 200m=3600m,通过此桥需要的时间为
 。
。
答案:240s出租车问题:
1.出租车的速度表示车辆行驶过程中的行进速度,指针指示的数值就是该时刻的速度值,采用的单位为km/h。
2.里程示数窗表示该车行驶的总路程,某段时间的路程就等于这段时间内两个示数的差。
3.出租车票据上给出的上车、下车时间间隔为车行驶时间,里程就是这段时间内出租车通过的路程。利用这些信息,可以解决与出租车有关的多种问题。例某人乘出租车时得到一张天津市客运出租行业专用发票,如表所示,此人乘车时间为____;该车这段时间内运动的平均速度为____km/h。

解析:根据出租车票据的起止时问,可以知道此人乘车时间为10min,出租车行驶的路程是5.5km,利用速度公式求出汽车的平均速度为: =33km/h。
=33km/h。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:汽车已进入普通家庭,汽车的前窗玻璃大多是“倾斜”的,这是因为只有这样,根据______成像特点,夜间车内乘客或其它物体所成的像在玻璃的______方(填“正前”或“前下”或“前上”).-物理
下一篇:小明同学身高1.5m,他站在平面镜前2m的地方,这个同学在平面镜中的像高______m,像与平面镜的距离为______m,这个同学向镜前移动0.5m,此时像与他的距离为______m,他向镜-物理
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |

![如图所示,在“探究平面镜成像特点”的实验中,下列说法正确的是[]A.为了便于观察,该实验最好在较暗的环境中进行B.B如果将蜡烛A向玻璃板靠近,像的大小会变大C.移去后面的蜡烛-九年级物理](http://www.00-edu.com/d/file/ks/wuli/1/27/2019-12-20/b491d9b8f9500ff2b6afefc8a8cb4cfb.png)
![视力检测时要求被测的人与视力表的距离为5m,如图所示,视力表与平面镜的距离是3m。为满足测量要求,人与平面镜的距离应为[]A.1mB.1.5mC.2mD.3m-八年级物理](http://www.00-edu.com/d/file/ks/wuli/1/27/2019-12-20/125b1d527847bef3113751c9f44bf1d2.gif)
![下列四组连线中,完全正确的是[]A.科学发现和科学家:杠杆原理→阿基米德;惯性定律→牛顿B.物理问题研究及科学方法:力的合成--控制变量法;研究电流跟电压.电阻的关系--等效-九年级物理](http://www.00-edu.com/d/file/ks/wuli/1/27/2019-12-20/e5877ad91a1ada5ea0d5610eff77d65b.png)