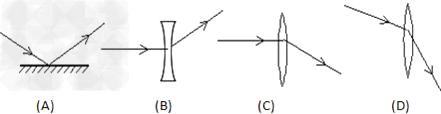
小明将物体放在离凸透镜10cm时,得到一个放大的倒立像;若将物体向凸透镜移近2cm,则可能得到一个A.较小的放大倒立像B.更大的放大倒立像C.放大的正立的像D.缩小的正立的像-八年级物理
题文
小明将物体放在离凸透镜10cm时,得到一个放大的倒立像;若将物体向凸透镜移近2cm,则可能得到一个
|
答案
| BC |
试题分析:凸透镜成像的大小由物距决定.解题时可通过物体在凸透镜前10cm处,能得到倒立放大的像,先推测出凸透镜焦距的大小,再比较物体移动后的新物距跟凸透镜焦距的大小,再次利用凸透镜成像条件判断成像的性质(当物距大于二倍焦距时,凸透镜成倒立缩小的实像;当物距等于二倍焦距时,凸透镜成倒立等大的实像;当物距大于一倍焦距小于二倍焦距时,凸透镜成倒立放大的实像;当物距小于一倍焦距时成正立放大的虚像). 物体在凸透镜前能成倒立放大的像,说明此时的物距大于一倍焦距小于二倍焦距,即:f<10cm<2f,所以凸透镜的焦距5cm<f<10cm. 物体在凸透镜前10cm处,将物体向透镜移近2cm后,则u=10cm-2cm=8cm, 此时有两种可能:①物距大于一倍焦距小于二倍焦距时,凸透镜成倒立放大的实像,此时的像将更大; ②物距小于一倍焦距,由凸透镜成像条件可知,得到的像是正立放大的虚像. 故选BC. 点评:此题主要考查凸透镜成像规律及其应用,能否通过物体成像的性质得出凸透镜的焦距范围是本题的突破点。 |
据专家权威分析,试题“小明将物体放在离凸透镜10cm时,得到一个放大的倒立像;若将物体..”主要考查你对 透镜及其分类 等考点的理解。关于这些考点的“档案”如下:
透镜及其分类
考点名称:透镜及其分类
- 透镜及透镜相关概念:
名称 概念 说明 透镜 透镜是利用光的折射来工作的光学元件,它是由透明物质(如玻璃、塑料、水晶等)制成的,表面是球面的一部分。如下图甲所示,中间厚、边缘薄的透镜叫凸透镜;如下图乙所示,边缘厚、中问薄的透镜叫凹透镜 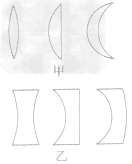
按其厚薄的形状可分为两类:凸透镜和凹透镜 主光轴 通过透镜两个球面球心的直线叫主光轴,如下图所示
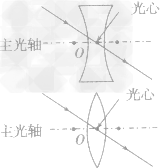
每个透镜都有一条主光轴 光心 主光轴上有个特殊的点,通过它的光线传播方向不改变,这个点叫做透镜的光心,如上图所示 用字母“O”表示,可以认为薄透镜的光心就在透镜的中心 焦点 凸透镜能使跟主光轴平行的光线会聚在主光轴上的一点,这一点叫凸透镜的焦点,如下图甲所示。凹透镜能使跟主光轴平行的光线通过凹透镜后变得发散,且这些发散光线的反向延长线相交在主光轴上一点,这一点不是实际光线的会聚点,所以叫凹透镜的虚焦点,如下图乙所示 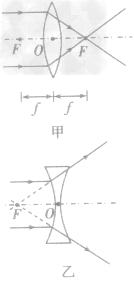
凸透镜两侧各有一焦点,且对称,用字母“F”表示 焦距 焦点到凸透镜光心的距离叫焦距,如上图甲所示 凸透镜两侧焦距相等,用字母“f” 表示 - 透镜及其应用知识梳理:
凸
透
镜定义:中间厚边缘薄的透镜 光学性质:对光线有汇聚作用 基本规律、概念 通过光心的光线不偏折 主光轴:两个球面所在球心的连线 平行于主光轴的入射光线会聚于焦点 焦距:焦点到光心的距离 成像规律 物距:u>2f,成缩小倒立的实像,像距:f<v<2f 物距:f<u<2f,成放大倒立的实像,像距:v>2f 物距:u<f,成放大正立的虚像 凹
透
镜定义:中间薄边缘厚的透镜 光学性质:对光线有发散作用 应
用日常生活 照相机:凸透镜成缩小实像的原理 投影仪:凸透镜成放大实像的原理 放大镜:凸透镜成放大虚像的原理 眼睛 眼睛成像原理:晶状体和角膜的组合相当于凸透镜 近视眼的矫正:佩戴凹透镜制成的近视镜 远视眼的矫正:佩戴凸透镜制成的远视镜 科技 望远镜 显微镜
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图甲所示,小文在探究凸透镜成像规律时,将凸透镜A固定在光具座上保持位置不变,使烛焰在光屏上成清晰的像。把烛焰与光屏的位置对换后,在光屏上将观察到倒立、(选填“放大-八年级物理
下一篇:小明用焦距为10cm的凸透镜做实验,实验装置如图所示,在实验过程中,他保持凸透镜的位置不变。(1)改变蜡烛的位置,使其位于10cm刻度时,再移动光屏,发现烛焰在光屏上的像位-八年级物理
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |