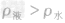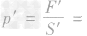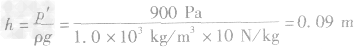如图所示是一种水闸,闸门的底部与铰轴O相连,厚度不计的闸门高为H、宽为a.AB为一根不计质量的杆,A端通过铰链与闸门相连,B端通过铰链与地面相连.杆AB与地面成60°角,A端距-物理
(1)求玻璃杯的重力。
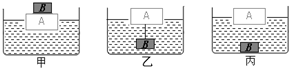
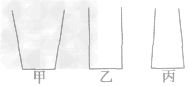
(2)在玻璃杯中装入1kg水后,水对杯底产,£的压强为900Pa,求水的深度;并通过计算推测出玻璃杯的大致形状是图中甲、乙、丙的哪一种?(水的密度p= 1.0×103k/m3,取g=10N/kg,杯壁的厚度可忽略)
解析:
(1)由
 得:玻璃杯的重力:
得:玻璃杯的重力:
(2)由
 得水的深度:
得水的深度:
假设杯壁是竖直的,装入1KG水后杯中水的深度应为:
 ,因为h'>h,所以水杯底小,口大,大致形状是甲图。
,因为h'>h,所以水杯底小,口大,大致形状是甲图。液体对容器底的压强、压力与容器对支持面的压强、压力的计算方法:
液体对容器底的压强和压力与容器对支持面的压强和压力不是一同事。
1.液体内部压强是由液体的重力产生的,但液体对容器底的压力并不一定等于液体的重力,而等于底面积所受的压强乘以受力面积,因此,处理液体内部问题时,先求压强再算压力。
2.容器对支持面的压力和压强,可视为固体问题 处理,先分析压力大小,再根据
 计算压强大小。
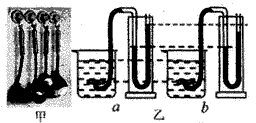
计算压强大小。例:如图所示,一开口的杯子,装上8cm高的水后,放在水平桌面上。已知杯子内部底面积为50cm2,外部底面积为60cm2;杯子装上水后的总质量为 0.6kg,则水对杯底的压力为___N,杯子对桌面的压强为_____Pa.

解析:从杯子的形状可知,杯中水对杯底的压力并小等于水的重力,要求液体对容器底的压力时,一般是先求出压强,再根据F=pS求压力,即F=pS=
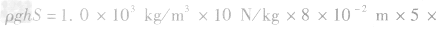 10-3m2=4N,而杯子对桌面的压力为杯与水的总重,即
10-3m2=4N,而杯子对桌面的压力为杯与水的总重,即 ,压强
,压强
 。
。答案:4N 1×103
考点名称:杠杆的动态平衡分析
杠杆的平衡状态:
杠杆静止不动或匀速转动都叫做杠杆平衡,注意我们在实验室所做的杠杆平衡条件的实验,是在杠杆水平位置平衡进行的,但在实际生产和生活中,这样的平衡是不多的,在许多情况下,杠杆是倾斜静止的,这是因为杠杆受到平衡力作用。所以说杠杆不论处于怎样的静止,都可以理解成处于平衡状态。杠杆动态平衡问题:
杠杆动态平衡的几种类型杠杆动态平衡是指构成杠杆的某些要素发生变化,而杠杆仍处于静止状态或匀速转动状态,
分析杠杆的动态平衡时,一般是动中取静,根据杠杆平衡条件,分析比较,得出结论。下面就杠杆动态平衡问题归类分析。
一、 阻力一定,判断动力的变化情况
1、l1不变,l2变化
例1、如图1所示,轻质杠杆可绕O转动,在A点始终受一垂直作用于杠杆的力,在从A转动A/位置时,力F将()
A、变大
B、变小
C、先变大,后变小
D、先变小,后变大
分析:当杠杆在水平面以下上升到水平面上时,l1不变,l2增大,由 ,F增大,当杠杆从水平面继续上升过程中,l2减小,所以F减小。
,F增大,当杠杆从水平面继续上升过程中,l2减小,所以F减小。
2、l2不变,l1变化
例2、如图2所示,轻质杠杆OA的B点挂着一个重物,A端用细绳吊在圆环M下,此时OA恰成水平且A点与圆弧形架PQ的圆心重合,那么当环M从P点逐渐滑至Q点的过程中,绳对A端的拉力大小将()
A、保持不变
B、逐渐增大
C、逐渐减小
D、由大变小再变大
分析:当M点从P点滑至Q点的过程中,我们分两个过程分析,
一是从P点滑至竖直位置,动力臂l1逐渐增大(同学们不妨作出这两点的动力臂),由 知F逐渐变小;
知F逐渐变小;
二是从竖直位置到Q点,动力臂逐渐减小,所以又逐渐增大。故选D。
3、l1与l2同时变化,但比值不变
例3、用图3所示的杠杆提升重物,设作用在A端的力F始终竖直向下,在将重物慢慢提升到一定高度的过程中,F的大小将()
A、保持不变
B、逐渐变小
C、逐渐变大
D、先变大,后变小
分析::F始终竖直向下,与阻力作用线平行,分别作出F与G的力臂l1和l2,构建两个相似三角形(同学们不妨在图中作出),可以看出, 为定值,由杠杆平衡条件,
为定值,由杠杆平衡条件, ,得
,得 ,所以,F大小不变。
,所以,F大小不变。
4、l1与l2同时变化
例4、如图4所示,一个直杠杆可绕轴O转动,在直杆的中点挂一重物,在杆的另一端施加一个方向始终保持水平的力F,将直杆从竖直位置慢慢抬起到水平位置过程中,力F大小的变化情况是()
A、一直增大
B、一直减小
C、先增大后减小
D、先减小后增大
分析:将直杆从竖直位置慢慢抬起到水平位置过程中,l1变小,l2变大,由 知,F一直在增大。
知,F一直在增大。
二、动力与阻力不变,动力臂与阻力臂变化
例5、如图5所示,用一细线悬挂一根粗细均匀的轻质细麦桔杆,使其静止在水平方向上, O为麦桔杆的中点.这时有两只蚂蚁同时从O点分别向着麦桔杆的两端匀速爬行,在蚂蚁爬行的过程中麦桔杆在水平方向始终保持乎衡,则()
A、两蚂蚁的质量一定相等
B、两蚂蚁的爬行速度大小一定相等
C、两蚂蚁的质量与爬行速度大小的乘积一定相等
D、两蚂蚁对麦桔杆的压力一定相等
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |