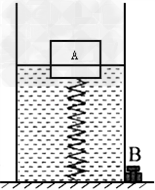
如图所示，底面积为200cm2的容器底部有一固定轻质弹簧，弹簧上方连有一边长为10cm的正方体木块A，容器侧面的底部有一个由阀门B控制的出水口，当容器中水深为20cm时，木块A有-八年级物理

首页 > 考试 > 物理 > 初中物理 > 液体压强的计算/2020-04-23 / 加入收藏 / 阅读 [打印]

题文

如图所示，底面积为200cm2的容器底部有一固定轻质弹簧，弹簧上方连有一边长为10cm的正方体木块A，容器侧面的底部有一个由阀门B控制的出水口，当容器中水深为20cm时，木块A有的体积浸在水中，此时弹簧恰好处于自然状态，没有发生形变．（不计弹簧受到的浮力，g取10N/kg）    求：
（1）此时容器底部受到的水的压强；
（2）木块A的密度；
（3）向容器内缓慢加水，直至木块A刚好完全浸没水中，立即停止加水，弹簧伸长了3cm，求此时弹簧对木块A的作用力F1是多大？容器底部受到水的压强变化了多少？
题型：计算题  难度：中档

答案

解：
（1）容器底部受到水的压强 p=ρ水gh=1×103kg/m3×10N/kg×0.2m=2×103Pa；     
（2）弹簧恰好处于自然状态时没有发生形变
F浮=G
ρ水gV排=ρ木gV木
ρ木= ρ水=0.4×103kg/m3；
（3）木块A刚好完全浸没水中
F1=F浮﹣G=ρ水gV﹣ρ木gV=1×103kg/m3×10N/kg×10﹣3m3﹣0.4×103kg/m3×10N/kg×10﹣3 m3
=6N；             
△h= ×10cm+3cm=9cm=0.09m； △p=ρ水g△h=1×103kg/m3×10N/kg×0.09m=900Pa．
答：（1）此时容器底部受到的水的压强为2×103Pa；
（2）木块A的密度为0.4×103kg/m3；
（3）此时弹簧对木块A的作用力F1是6N；容器底部受到水的压强变化了900Pa．

据专家权威分析，试题“如图所示，底面积为200cm2的容器底部有一固定轻质弹簧，弹簧上方..”主要考查你对  液体压强的计算，物体的浮沉条件及其应用  等考点的理解。关于这些考点的“档案”如下：

液体压强的计算物体的浮沉条件及其应用

考点名称：液体压强的计算

  • 液体压强的计算公式：
    P=ρgh（ρ是液体密度，单位是千克/米3；g=9.8牛/千克；h是深度，指液体自由液面到液体内部某点的竖直距离，单位是米。）

  • 对液体压强公式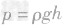的理解
    1．由公式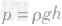可知，液体内部的压强只跟液体的密度和深度有关，而跟液体的质量、重力、体积以及容器的形状、底面积等无关。

    2．公式只适用于计算静止的液体产生的压强，而对固体、气体或流动的液体均不适用。

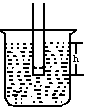
    3．在液体压强公式中h表示深度，而不是高度。判断出h的大小是计算液体压强的关键，如图所示，甲图中A点的深度为30cm，乙图中B点的深度为 40cm．丙图中C点的深度为50cm。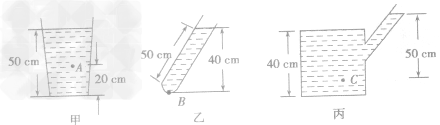

    4．运用公式时应统一单位：ρ的单位用kg／m3，h 的单位用m，计算出的压强单位才是Pa。 

    5．两公式的区别与联系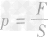：是压强的定义式，  无论固体、液体还是气体，它都是普遍适用的；而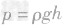是结合液体的具体情况通过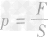推导出来的，所以适用于液体。

    6．用公式求出的压强是液体由于自身重力产生的压强，它不包括液体受到的外加压强。

    转换法和控制变量法探究液体压强大小跟哪些因素有关：
         在探究液体压强的大小时，由于液体压强的大小不易测量或是不能直接观测到它的大小，我们用“转换法”，通过液体压强计中两玻璃管液面的高度差的大小来比较液体压强的大小，将抽象的东西变成了直观且形象的东两，使问题简化了。

        由于液体内部压强跟液体的深度和液体密度两方面因素有关，所以在探究液体内部压强的规律时要采用控制变量法，即在探究液体压强与深度的关系时，要保持液体密度不变，在探究液体压强与液体的密度关系时，要保持液体的深度不变。

考点名称：物体的浮沉条件及其应用