如图是利用电子秤显示水库水位装置的示意图。该装置主要由不计重力的滑轮C、D,长方体物块A、B以及轻质杠杆MN组成。物块A通过细绳与滑轮C相连,物块B通过细绳与杠杆相连。杠-九年级物理
题文
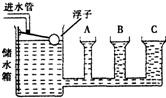
如图是利用电子秤显示水库水位装置的示意图。该装置主要由不计重力的滑轮C、D,长方体物块A、B以及轻质杠杆MN组成。物块A通过细绳与滑轮C相连,物块B通过细绳与杠杆相连。杠杆可以绕支点O在竖直平面内转动,杠杆始终在水平位置平衡,且MO:ON=1:2。已知物块A的密度为1.5×103kg/m3,底面积为0.04m2,高1 m,物块B的重力为100N。滑轮与转轴的摩擦、杠杆与轴的摩擦均忽略不计,求: (1)当物块A的顶部刚没入水面时,底部受到水的压强大小; (2)当物块A的顶部刚没入水面时,物块A所受的拉力大小;
|
答案
(1) Pa (2)200 (3)0.3m Pa (2)200 (3)0.3m |
试题分析:当A的表面刚没入水面时,知道底部所处的深度,根据p=ρgh求出底部受到水的压强;当物块A的顶部刚没入水面时,知道物块A的底面积和高,可求出物块A的体积,由于是没入,所以排开液体的体积求出来了,根据F浮=ρ水V排g求出物块A受到的浮力,再根据F拉=GA-F浮求出物块A受到的拉力;先根据F示=GB-FN,求出杠杆N端受到的拉力,根据杠杆的平衡条件求出杠杆M端受到的拉力;根据动滑轮的特点求出滑轮组对A的拉力;然后根据阿基米德定律的变形公式求出排开液体的体积,用体积除以底面积求出深度。 (1)当物块A的顶部刚没入水面时,底部所处的深度: h=1m, 底部受到水的压强: p=ρgh=1×103kg/m3×10N/kg×1m=1×104Pa. (2)物块A的体积: VA=0.04m2×1m=0.04m3, 物体A重: GA=ρAVAg=1.5×103kg/m3×0.04m3×10N/kg=600N, ∵物块A没入水中, ∴排开水的体积: V排=VA=0.04m3, 物块A所受的浮力: F浮=ρ水V排g=1×103kg/m3×0.04m3×10N/kg=400N; 物块A所受的拉力: F拉=GA-F浮=600N-400N=200N; (3)①电子秤的示数F示=GB-FN,则杠杆N端受到的拉力: FN=GB-F示=100N-40N=60N, ∵杠杆平衡,MO:ON=1:2 ∴FMLOM=FNLON, ∴杠杆M端受到的拉力: FM=120N; ②滑轮与转轴的摩擦、杠杆与轴的摩擦均忽略不计, 滑轮D受到向下的拉力: FD=2FM=2×120N=240N, 滑轮C受到向下的拉力: FC=2FD=2×240N=480N, ∴滑轮组对A的拉力: F拉A=FC=480N; ③∵F拉A+F浮=GA, ∴F浮=GA-F拉A=ρAVAg-F拉A=1.5×103kg/m3×0.04m3×10N/kg-480N=600N-480N=120N, ∵F浮=ρ水V排g, ∴  , ,∵V排=Sh浸, ∴物块A浸入水中的深度: h浸=  点评:此题是一道综合性试题,结合浮力的计算和杠杆的平衡条件等知识点,难度较大 |
据专家权威分析,试题“如图是利用电子秤显示水库水位装置的示意图。该装置主要由不计重..”主要考查你对 液体压强的计算 等考点的理解。关于这些考点的“档案”如下:
液体压强的计算
考点名称:液体压强的计算
- 液体压强的计算公式:
P=ρgh(ρ是液体密度,单位是千克/米3;g=9.8牛/千克;h是深度,指液体自由液面到液体内部某点的竖直距离,单位是米。) 对液体压强公式
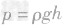 的理解
的理解
1.由公式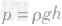 可知,液体内部的压强只跟液体的密度和深度有关,而跟液体的质量、重力、体积以及容器的形状、底面积等无关。
可知,液体内部的压强只跟液体的密度和深度有关,而跟液体的质量、重力、体积以及容器的形状、底面积等无关。
2.公式只适用于计算静止的液体产生的压强,而对固体、气体或流动的液体均不适用。
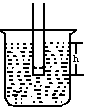
3.在液体压强公式中h表示深度,而不是高度。判断出h的大小是计算液体压强的关键,如图所示,甲图中A点的深度为30cm,乙图中B点的深度为 40cm.丙图中C点的深度为50cm。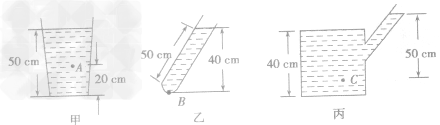
4.运用公式时应统一单位:ρ的单位用kg/m3,h 的单位用m,计算出的压强单位才是Pa。
5.两公式的区别与联系: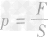 是压强的定义式, 无论固体、液体还是气体,它都是普遍适用的;而
是压强的定义式, 无论固体、液体还是气体,它都是普遍适用的;而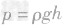 是结合液体的具体情况通过
是结合液体的具体情况通过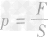 推导出来的,所以适用于液体。
推导出来的,所以适用于液体。 6.用公式求出的压强是液体由于自身重力产生的压强,它不包括液体受到的外加压强。
转换法和控制变量法探究液体压强大小跟哪些因素有关:
在探究液体压强的大小时,由于液体压强的大小不易测量或是不能直接观测到它的大小,我们用“转换法”,通过液体压强计中两玻璃管液面的高度差的大小来比较液体压强的大小,将抽象的东西变成了直观且形象的东两,使问题简化了。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |