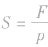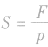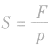下表是某四轮轿车的部分数据,图是该轿车发动机的能量流向图.(1)该小汽车静止在水平地面上时,对地面的压强是多大?(2)若该小汽车行驶100km.则需耗油多kg?(1L=10-3m3)(3)假若-物理
答案:C
考点名称:功的计算
- 功的计算公式:
功(W)等于力(F)跟物体在力的方向上通过的距离(s)的乘积。(功=力×距离),W=FS。
单位:
国际单位制中,力的单位是N,距离的单位是m,功的单位是N·m,它有一个专用名称叫做焦耳,简称焦,用符号J表示,1J=1N·m。 - 在利用该公式进行计算时的注意点:
(1)力与物体移动的距离在方向上必须一致;
(2)力与物体移动的距离必须对应于同一物体;
(3)力与物体移动的距离必须对应于同一段时间。
考点名称:机械效率的计算
- 机械效率的定义:
有用功跟总功的比值叫做机械效率;
计算公式:
η=
- 机械效率的意义:
(1)机械效率的功率是标志机械做功性能好坏的物理量,机械效率越高,这个机械的性能越好。
(2)机械效率的高度并不决定使用机械是省力还是费力,效率高只说明有用功在总功所占的比例;省力还是费力是指做一定的有用功时,所用动力的大小。机械效率高不一定省力。 - 功,功率和机械效率的比较:
物理量 物理意义 定义 符号 公式 单位 说明 功 做功即能量的转化 有力作用在物体上,并且物体在力的方向上移动了一段距离,就说力对物体做了功 W W=Fs J l. 功率大小由功和时间共同决定,单独强调某一方面是错误的 2.功率和机械效率是两个不同的物理量,它们之问没有直接关系 功率 做功快慢 单位时间内完成的功 P 
W(国际单位)
kW,MW(常用单位)机械效率 反映机械性能的物理量 有用功占总功的总值 η 
无 - 汽车的机械效率和功率:
机械效率与功率是两个完全不同的概念。
这两个物理量是从不同方面反映机械性能的,它们之间没有必然的联系。
功率大表示机械做功快;机械效率高表示机械对总功的利用率高。功率大的机械不一定机械效率高。内燃机车功率可以达到几千千瓦,但效率只有30%r~ 40%,反之,机械效率高的机械功率不一定大。安装在儿童玩具汽车里的电动机效率可达80%,但功率却只有凡瓦特。
考点名称:密度公式的应用
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比 。
。- 密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ = 总结规律后方可。
总结规律后方可。
如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为 ,ρ乙=
,ρ乙=  ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
2. 密度公式ρ = 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:
密度的公式是ρ = ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:植树节里,小倩同学用水桶提了15L水给刚栽上的树浇水,桶中水深为30cm.(g取10N/kg)求:(1)15L水的质量是多少?(2)水对桶底的压强多大?-物理
下一篇:如图所示,物体A重30N,B重15N,物体A的底面积为10cm2,物体B的底面积为5cm2.则A对B的压强是______Pa,B对桌面的压强是______Pa.-物理
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |

![将下图所示的长方体,从中间切开变成完全相同的两块,并将一块按照图中所示放在另一块的上面。若长方体放在水平桌面上,则长方体对桌面的前、后两次压强之比P1∶P2为[]A、1∶1-八年级物理](http://www.00-edu.com/d/file/ks/wuli/1/118/2020-05-27/678b8740a9b334137d65f7a73524e729.gif)