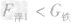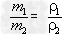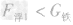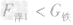一个体积是1.0×10-3米3的铁球挂在弹簧秤上,若将铁球浸没在水中,此时弹簧秤的示数是铁球在空气中示数的4/5,求:(1)铁球受到的浮力;(2)铁球受到的重力;(3)这个铁球是空心-八年级物理
3=50cm3 =5.0×10-5m3
得 =84t
=84t
答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3, =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1= ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2= ,合金的体积
,合金的体积 ,则合金的密度
,则合金的密度
在(2)中两种金属的体积相等,设为 ,合金的体积
,合金的体积 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1= ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为 ,合金的质量m总
,合金的质量m总 ,合金的密度为
,合金的密度为 。
。
答案:
注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
得
 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3, =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2= ,合金的体积
,合金的体积 ,则合金的密度
,则合金的密度
在(2)中两种金属的体积相等,设为
 ,合金的体积
,合金的体积 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1= ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为 ,合金的质量m总
,合金的质量m总 ,合金的密度为
,合金的密度为 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
考点名称:力的合成与应用
- 定义:
几个力共同作用在一个物体上时,它们的作用效果可以用一个力来代替,这个力就称为那几个力的合力。如果已知几个力的大小和方向,求合力的大小和方向,称为力的合成。
说明:
合力是为了表示几个力的作用效果而引入的,它并不是存存于物体受到的几个力之外的力,而是为了简化物体受到的各个力的一种方法,因此力的合成称为等效替代法。 - 同一直线上二力的合成:
1.同一直线上同方向二力的合力,大小等于二力大小之和,方向与这两个力方向相同。记作:F=F1+F2。如图所示,既有人在车前拉,又有人在车后推,车同时受到拉力F1和推力F2的作用,并且这两个力方向相同则拉力和推力的合力大小F=F1+F2.
2.同一直线上相反方向的二力的合力,大小等于二力大小之差的绝对值,方向和较大的力的方向相同。记作:F=|F1一F2|。
不同直线上的两个力合成:
两个力合成时,以表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向,这就叫做平行四边形定则。
力的平行四边形定则以此得证:
(1)两分力大小不变时,夹角越大,合力越小
(2)合力大小的变化范围F1+F2≥F≥|F1-F2|
(3)力的合成的平行四边形定则,只适用于共点力(结论)
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:潜水艇在水面上的排水量是3000t,在水下的排水量是3800t,当潜水艇在水面航行时,水上部分的体积是_________m3;若潜入水中时,应吸入水_________kg.(g=10N/kg)-九年级物理
下一篇:一个物体重11N,体积为1dm3,如果将它浸没在水中,它受到的浮力是N,若将该物体投入密度1.2×103kg/m3的足够深的盐水中,静止时受到的浮力是N。-八年级物理
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |