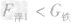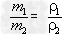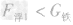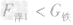一密度为ρ木=0.6×103㎏/m3的长方形木块,长a=0.4m,宽b=0.2m,高c=0.1m.(1)当木块漂浮在水面上时,它露出水面部分的体积是多少?(2)若用挖空的办法,把这个木块做成一只小-物理
题文
| 一密度为ρ木=0.6×103㎏/m3的长方形木块,长a=0.4m,宽b=0.2m,高c=0.1m. (1)当木块漂浮在水面上时,它露出水面部分的体积是多少? (2)若用挖空的办法,把这个木块做成一只小“船”,使它能装载5.9㎏的沙子而不至于沉没,木块上被挖去的那部分体积至少应该有多大?(水的密度ρ水=1×103㎏/m3,g取10N/㎏) |
答案
| (1)木块的体积为:V=abc=0.4m×0.2m×0.1m=0.008m3 木块的重力为:G木=mg=ρ木gV=0.6×103㎏/m3×10N/kg×0.008m3=48N 因为木块漂浮,所以F浮=G木=48N 根据F浮=ρ水gV排得,V排=
露出水面部分的体积是V露=8×10-3m3-4.8×10-3m3=3.2×10-3m3. 答:露出水面的体积为3.2×10-3m3. (2)当木块完全浸没时所受的浮力为:F浮′=ρ水gV=1.0×103kg/m3×10N/kg×0.008m3=80N 剩下的木块与沙子的重力为:G总=F浮=80N 所以剩下木块的质量为:m剩=
剩余木块的体积为:V剩=
所以挖去木块的体积为:V挖=0.008m3-
答:挖去的那部分体积至少为4.5×10-3m3. |
据专家权威分析,试题“一密度为ρ木=0.6×103㎏/m3的长方形木块,长a=0.4m,宽b=0.2m,..”主要考查你对 浮力及阿基米德原理,物体的浮沉条件及其应用 等考点的理解。关于这些考点的“档案”如下:
浮力及阿基米德原理物体的浮沉条件及其应用
考点名称:浮力及阿基米德原理
- 浮力:
(1)定义:浸在液体中的物体受到向上托的力叫做浮力。
(2)施力物体与受力物体:浮力的施力物体是液体 (或气体),受力物体是浸入液体(或气体)中的物体。
(3)方向:浮力的方向总是竖直向上的。
阿基米德原理:
(1)原理内容:浸在液体里的物体受到液体竖直向上的浮力,浮力的大小等于它排开的液体受到的重力。
(2)公式: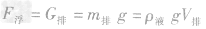 ,式中ρ液表示液体的密度,V排是被物体排开的液体的体积,g取9.8N/kg。
,式中ρ液表示液体的密度,V排是被物体排开的液体的体积,g取9.8N/kg。 - 浮力大小跟哪些因素:
有关浸在液体中的物体受到浮力的大小,跟物体浸入液体中的体积有关,跟液体的密度有关,跟物体浸入液体中的深度无关。跟物体本身密度大小无关。 - 阿基米德原理的五点透析:
(1)原理中所说的“浸在液体里的物体”包含两种状态:一是物体的全部体积都浸入液体里,即物体浸没在液体里;二是物体的一部分体积浸入液体里,另一部分露在液面以上。
(2)G排指被物体排开的液体所受的重力,F浮= G排表示物体受到的浮力的大小等于被物体排开的液体的重力。
(3)V排是表示被物体排开的液体的体积,当物体全部浸没在液体里时,V排=V物;当物体只有一部分浸入液体里时,则V排<V物。
(4)由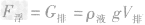 可以看出,浮力的大小只跟液体的密度和物体排开液体的体积这两个因素有关,而跟物体本身的体积、密度、形状、在液体中的深度、液体的多少等因素无关。
可以看出,浮力的大小只跟液体的密度和物体排开液体的体积这两个因素有关,而跟物体本身的体积、密度、形状、在液体中的深度、液体的多少等因素无关。
(5)阿基米德原理也适用于气体,但公式中ρ液应该为ρ气。
控制变量法探究影响浮力大小的因素:
探究浮力的大小跟哪些因素有关时,用“控制变量法”的思想去分析和设计,具体采用“称量法”来进行探究,既能从弹簧测力计示数的变化中体验浮力,同时,还能准确地测出浮力的大小。
例1小明在生活中发现木块总浮在水面,铁块却沉入水底,因此他提出两个问题:
问题1:浸入水中的铁块是否受到浮力?
问题2:浮力大小与哪些因素有关?
为此他做了进一步的猜想,设计并完成了如图所示实验,
(1)(b)、(c)图中弹簧测力计示数均小于(a)图中弹簧测力计示数,说明浸入水中的铁块__(选填 “受到”或“不受到”)浮力;
(2)做___(选填字母)两次实验,是为了探究铁块浸没在水中时所受浮力大小与深度是否有关;
(3)做(d)、(e)两次实验,是为了探究浮力大小与 __的关系。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:现提供如下器材:正方体物块(密度大于水的密度)、天平(附砝码)、弹簧测力计、溢水杯、烧杯、刻度尺、细线、水(水的密度ρ水已知).根据以上器材可以设计多个实验,如下表中的示-物理
下一篇:有一体积为1×10-4米3的实心铁块,挂在弹簧秤上后浸没在水中(铁块没有接触容器底部),铁的密度为7.8×103千克/米3,求:(1)铁块的重力.(2)铁块所受到的浮力.(3)弹簧秤的示数.-物理
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |