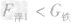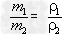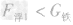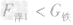婵犵數濮甸鏍窗濡ゅ懏鏅梻浣割吔閺夊灝顬堥柛妤呬憾閺岀喖姊荤€电ǹ濡介梺绋垮閸ㄥ潡寮诲☉婊呯杸闁哄洨鍋涙禒姗€姊哄Ч鍥у闁稿鎸荤粚杈ㄧ節閸ヨ埖鏅梺鎸庣箓鐎氼參宕愰敐鍥╃=濞达絼绮欓崫铏圭磼鐠囨彃顏紒鍌涘浮閺佸倿鎳為妷褏肖闂備線娼ц効闁逞屽墴閺佸啴宕掑☉姘箺婵$偑鍊曠换鎰偓姘槻鍗遍柟闂寸劍閻撴洟鏌曡箛銉х?闁告瑢鍋撻梻浣侯攰濞呮洖煤閺嶎叏缍栨繝闈涱儏鍞梺闈涚箳婵櫕绔熼弴銏♀拺缂佸瀵у﹢鏉裤€掑顓ф疁鐎规洘娲栭~婊堝焵椤掆偓椤繑绻濆顒傦紲闂侀潧鐗嗛幊蹇涙倶閺囩儐娓婚柕鍫濆暙閻忣亪鏌涢妸銉ヮ暢缂侇喖顑呴鍏煎緞婵犱胶鐐婇梻浣告啞濞诧箓宕戦崱娑辨晩鐎光偓閸曨兘鎷绘繛鎾磋壘濞层倕顕g捄銊х=鐎广儰绀佹禍鍓х磽閸屾瑧鍔嶆慨濠傤煼瀹曚即寮介鐐寸€悗骞垮劚椤︿即宕戦崟顖涚厽闁瑰鍋嶇紓姘舵煟閿濆棗鈻曟慨濠傛惈鐓ら悹浣芥珪閹癸綁姊虹粙娆惧剱闁告梹娲熼崺銏ゅ籍閸繄鍘搁梺鍛婁緱閸犳牠宕滈鈧娲礈閹绘帊绨肩紓浣筋嚙缁夋潙宓勯梻渚囧墮缁夌敻鎮¤箛娑欑厱闁斥晛鍠氬▓鏃堟煃瑜滈崜婵嬶綖婢舵劕鐤鹃柛顐f礃閸嬫劙鏌ц箛锝呬簻鐎殿喖娼¢弻锝嗘償椤栨粎校闂佸摜濮电敮鈥崇暦閹达箑绠婚悗娑櫭鎾绘煟閻斿摜鎳冮悗姘噹椤繃娼忛妸銉︾€鹃梻浣虹帛椤ㄥ懘鎮ч崱娑欑厒婵犲﹤鎳愮壕濂稿级閸稑濡跨紒鐘靛仧閳ь剝顫夊ú鈺冪礊娴e摜鏆﹀┑鍌溓瑰敮闂侀潧绻掓慨铏珶閺囩喓绠鹃弶鍫濆⒔閸掍即鏌熺拠褏绡€鐎规洘鍨佃灒闁稿繒鍘ч弸鎴︽⒑缂佹﹩娈旈柣妤€妫涚划顓㈠箳閹垮啯顔旈梺缁樺姇閻°劌鐣风仦瑙f斀闁斥晛鍟亸锔锯偓瑙勬礃鐢帡鍩為幋锕€骞㈤柍琛″亾闁瑰鍏樺缁樻媴閸涘﹤鏆堥柣銏╁灣閸嬬偤寮茬捄浣曟棃宕ㄩ鐓庡婵犵數鍋涘Λ娆撳箰閸濄儲鍏滈柍褜鍓欓埞鎴炲箠闁稿﹥娲滈埀顒佸嚬閸撶喎鐣风憴鍕缂侇垱娲橀~宥夋⒑閻熸澘鈷旀い鎺撶叀瀵劎绱掑Ο鍦畾閻庣懓澹婇崰鏍ㄦ櫠閹绢喗鐓涘ù锝呮憸鑲栨繛瀵稿缁犳捇骞愭繝鍐ㄧ窞鐎光偓鐎n剛顦板┑鐘垫暩閸嬬偤宕归崼鏇炵缂佸锛曞ú顏勎у璺猴功椤斿棙绻涢弶鎴濇倯婵炲吋鐟╁畷锝嗙節閸ャ劎鍘繝銏f硾閻楀棝鍩€椤掍緡娈樼紒顔芥瀹曞ジ寮撮悢鍝勫妇闂備胶纭跺Σ鍛村储閻e备鍋撳鐐
一个空心铜球质量为89g,它能漂浮在水中,且有1/3个球露在水面上,已知铜的密度为8.9×103kg/m3,则此铜球的体积为______cm3,其空心部分的体积为______cm3.-物理

②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比
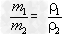 ;
;④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比
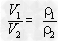 。
。1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
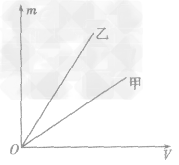
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ =
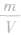 总结规律后方可。
总结规律后方可。如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
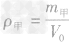 ,ρ乙=
,ρ乙= 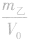 ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。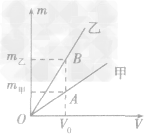
2. 密度公式ρ =
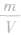 及变形
及变形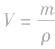 、m=ρV的应用:
、m=ρV的应用:密度的公式是ρ =
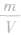 ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式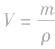 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
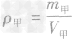 ,
,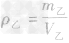
(2)写出该物理量比的表达式:
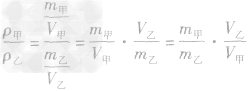
(3)化简:代入已知比值的求解:
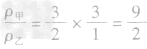
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10-5m3
得
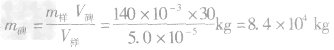 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
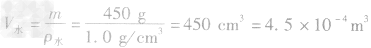 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为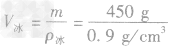 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3,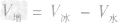 =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
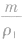 ,密度为ρ2的金属的体积V2=
闂備胶鍎甸崜婵堟暜閹烘绠犻幖杈剧悼閸楁岸鏌ら崫銉︽毄闁荤喎缍婇弻娑⑩€﹂幋婵囩亪闂佺粯甯楀浠嬬嵁閺嶎偀鍋撳☉娅辨粍绂掗敂鍓х<婵°倐鍋撻柟铏悾鐑芥晸閻樻彃宓嗗┑顔矫畷顒勫几閻樼粯鈷戦悹鍥b偓宕囦紙闂佺懓鍤栭幏锟� 濠电姵顔栭崳顖滃緤閻e本宕查柟鐗堟緲妗呮繝銏f硾椤戞垹妲愰敐澶嬬厱闁斥晛鍠氬▓鏃傜磼閹绘帗鍋ラ柡灞剧洴楠炴帒鈹戦崱鏇炴瀳闂備浇妗ㄧ粈渚€鏁冮妷銉$細濠电姵鑹鹃悙濠傤渻鐎n亝鎹fい锔诲櫍濮婃椽宕ㄦ繝搴㈢暦濠电偛寮堕悧鏇㈡偩閻戣姤鍋勭紒瀣儥閸ゃ倕鈹戦埥鍡楃仴妞ゆ泦鍥х闁哄洨浼濋悷鎵冲牚閹肩补鈧尙鏆楃紓鍌欑劍椤ㄥ懘藝闂堟稓鏆﹂柟杈鹃檮閺呮悂鏌ㄩ悤鍌涘
,密度为ρ2的金属的体积V2=
闂備胶鍎甸崜婵堟暜閹烘绠犻幖杈剧悼閸楁岸鏌ら崫銉︽毄闁荤喎缍婇弻娑⑩€﹂幋婵囩亪闂佺粯甯楀浠嬬嵁閺嶎偀鍋撳☉娅辨粍绂掗敂鍓х<婵°倐鍋撻柟铏悾鐑芥晸閻樻彃宓嗗┑顔矫畷顒勫几閻樼粯鈷戦悹鍥b偓宕囦紙闂佺懓鍤栭幏锟� 濠电姵顔栭崳顖滃緤閻e本宕查柟鐗堟緲妗呮繝銏f硾椤戞垹妲愰敐澶嬬厱闁斥晛鍠氬▓鏃傜磼閹绘帗鍋ラ柡灞剧洴楠炴帒鈹戦崱鏇炴瀳闂備浇妗ㄧ粈渚€鏁冮妷銉$細濠电姵鑹鹃悙濠傤渻鐎n亝鎹fい锔诲櫍濮婃椽宕ㄦ繝搴㈢暦濠电偛寮堕悧鏇㈡偩閻戣姤鍋勭紒瀣儥閸ゃ倕鈹戦埥鍡楃仴妞ゆ泦鍥х闁哄洨浼濋悷鎵冲牚閹肩补鈧尙鏆楃紓鍌欑劍椤ㄥ懘藝闂堟稓鏆﹂柟杈鹃檮閺呮悂鏌ㄩ悤鍌涘
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:一个体积为80cm3的物块,漂浮在水面上时,有36cm3的体积露出水面,试问:(l)物块所受浮力为多少?(2)物块的密度为多少?(ρ水=1.0×1O3kg/m3,g=10N/kg)-物理
下一篇:一块铁球在空气中称得重为45N,把它浸没在水中弹簧测力计的示数为32N,则铁球受到的浮力为______.-物理
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |