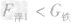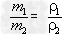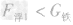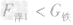将质量相等的实心铁球和铝球分别挂在等臂杠杆的两端,若将两球同时浸没水中,则()A.杠杆仍平衡B.杠杆失去平衡,马上又恢复平衡C.杠杆失去平衡,挂铝块的那端下沉D.杠杆失去平-物理
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2= ,合金的体积
,合金的体积 ,则合金的密度
,则合金的密度
在(2)中两种金属的体积相等,设为
 ,合金的体积
,合金的体积 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1= ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为 ,合金的质量m总
,合金的质量m总 ,合金的密度为
,合金的密度为 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
考点名称:杠杆的平衡条件
杠杆的平衡条件:
动力×动力臂=阻力×阻力臂。
即
在杠杆平衡时,动力臂是阻力臂的几倍,动力就是阻力的几分之几。利用杠杆平衡条件来分析和计算有关问题,一般遵循以下步骤:
(1)确定杠杆支点的位置。
(2)分清杠杆受到的动力和阻力,明确其大小和方向,并尽可能地作出力的示意图。
(3)确定每个力的力臂。
(4)根据杠杆平衡条件列出关系式并分析求解。
例:如图所示,AOB为一机械设备的简化示意图,我们可以把它看成杠杆(自重不计),已知AO= 2OB。固定D点,使OB处于水平位置,此时B端挂一重为40N的物体,要使杠杆不发生转动,至少需在A端施加F=____N的力,在图上画出此时力F的方向。
解析:要想得到施加在A点的最小力,就要找到最大力臂,由图可知,最大力臂应是OA,故过A点作们的垂线,方向斜向下即为最小力。据杠杆平衡条件得:F·OA=G·OB,代入数值为F×2OB=40N×OB,解方程得F=20N。
答案:20 力F的方向如图
实验法探究杠杆平衡条件:
实验前要调节杠杆的平衡螺母使其在水平位置上平衡,目的是使杠杆的重心落在支点上,从而消除杠杆的重力对平衡的影响。当杠杆水平平衡时,O点距悬挂钩码处的距离便是力臂,而且可用杠杆上的“格数”代替力臂大小。
例:我们都做过“探究杠杆平衡条件”的实验。
(1)实验没有挂钩码时,若杠杆左端下倾,则应将右端的平衡螺母向____(选填“左”或“右”)调节,使杠杆在水平位置平衡。实验前使杠杆水平平衡的目的是____.
(2)实验中,用图所示的方式悬挂钩码,杠杆也能水平平衡(杠杆上每格等距),但老师却提醒大家不要采用这种方式。这主要是因为该种方式( )
A.一个人无法独立操作
B.需要使用太多的钩码
C.力臂与杠杆不重合
D.力和力臂数目过多
(3)图中,不改变支点O右侧所挂的两个钩码及其位置,保持左侧第____格的钩码不动,将左侧另外两个钩码改挂到它的下方,杠杆仍可以水平平衡。
解析:(1)实验前要调节杠杆的平衡螺母使其在水平位置平衡,目的是方便地测量力臂。调节方法是将平衡螺母向杠杆偏高的一端调,即哪端轻向哪端调。
(2)探究杠杆平衡条件时,用的力和力臂数目过多,每个力都会给杠杆转动带来影响,给探究过程带来麻烦。
(3)根据杠杆平衡条件 ,即
,即
 ,所以l1=2(格)。
,所以l1=2(格)。
答案:(1)右方便地测量力臂(2)D(3)2利用杠杆平衡条件求最小力的方法:
由公式 可知,当阻力、阻力臂一定时,动力臂越长,动力越小。当动力臂最长时,动力最小。要求最小动力,必须先画出最大动力臂。
可知,当阻力、阻力臂一定时,动力臂越长,动力越小。当动力臂最长时,动力最小。要求最小动力,必须先画出最大动力臂。
1.寻找最大动力臂的方法
(1)当动力作用点确定后,支点到动力作用点的线段即为最大动力臂;
(2)动力作用点没有规定时,应看杠杆上哪一点离支点最远,则这一点到支点的距离即为最大动力臂。
2.作最小动力的方法
(1)找到最大动力臂后,过作用点作动力臂的垂线;
(2)根据实际,动力能使杠杆沿阻力作用的反方向转动,从而确定动力的方向。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |