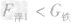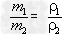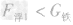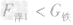一金属块在空气中受到的重力为39N,把它全部浸没水中称时(金属块未接触底面),弹簧测力计读数为34N.(g取10N/kg).求:(1)该金属块受到水对它的浮力?(2)该金属块的体积?(3)该金-物理
例1在探究“浮力大小等于什么”的实验中,小明同学的一次操作过程如图所示。
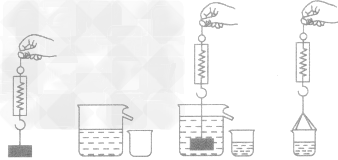
(1)测出铁块所受到的重力G铁;
(2)将水倒入溢水杯中;
(3)把铁块浸入溢水杯中,读出弹簧测力计示数F;
(4)测出小桶和被排开水的总重力G;
(5)记录分析数据,归纳总结实验结论,整理器材。
分析评估小明的实验,指出存在的问题并改正。
解析:在探究“浮力大小等于什么”的实验中,探究的结论是浮力的大小等于物体排开的液体所受到的重力,所以实验时,需要用弹簧测力计测出铁块受到的浮力和它排开水的重力进行比较得出结论,因此实验过程中需要测空小桶的重力G桶,并且将溢水杯中的水加至溢水口处。
答案:存在的问题:
(1)没有测空小桶的重力 (2)溢水杯的水量不足
改正:(1)测空小桶的重力G桶(2)将溢水杯中的水加至溢水口处

例曹冲利用浮力知识,巧妙地测出了大象的体重。请你写出他运用的与浮力有关的知识_____、 ____,另外,他所用到的科学研究方法是:_____和______.
解析:曹冲称象的过程是首先把大象放在船上,在水面处的船舷上刻一条线,然后把大象牵上岸。再往船上放入石块,直到船下沉到船舷上的线再次与水面相平时为止,称出此时船上石头的质量即为大象的质量。两次船舷上的线与水面相平,根据阿基米德原理可知,为了让两次船排开水的体积相同,进而让两次的浮力相同,再根据浮沉条件,漂浮时重力等于浮力可知:船重+大象重=船重+石头重,用多块石头的质量替代了不可拆分的大象的质量,这是等效替代法在浮力中的一个典型应用。
答案:浮沉条件 阿基米德原理 等效替代法化整为零法
考点名称:密度公式的应用
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比 。
。- 密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ = 总结规律后方可。
总结规律后方可。
如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为 ,ρ乙=
,ρ乙=  ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
2. 密度公式ρ = 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:
密度的公式是ρ = ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式: ,
,
(2)写出该物理量比的表达式:
(3)化简:代入已知比值的求解:
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:孙晓同学在家中利用身边的物品探究浮力的有关因素时,他把木块压入水中后松开手,发现木块又浮了上来,由此他得出浮力的大小与物体浸没在液体中的深度有关的结论.请你利用弹-物理
下一篇:有一种纪念币,它的质量是16.1克.为了测量它的体积,把它放入一盛满水的量筒中,测得溢出的水重为1.8×10-2牛.(1)求制作纪念币的金属密度;(2)说这种金属的名称;(3)盛满水-物理
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |