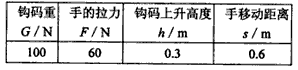
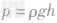节能是汽车性能的一个重要指标.但同一辆汽车每百公里的消耗与行驶速度的快慢是否有关呢?星期天,小明乘坐叔叔的汽车去上海,于是他决定借此机会对这一问题进行探究,他们去时-九年级物理
题文
| 节能是汽车性能的一个重要指标.但同一辆汽车每百公里的消耗与行驶速度的快慢是否有关呢?星期天,小明乘坐叔叔的汽车去上海,于是他决定借此机会对这一问题进行探究,他们去时走高速公路,回来时走320国道,得到了下表所示的数据. |
 |
| (1)分析数据后,小明觉得这与他事先的猜想吻合.你认为小明的猜测应该是________; (2)请你算出汽车在高速公路上行驶108 km消耗的汽油质量(  汽油=0.8kg/L); 汽油=0.8kg/L);(3)若汽车在高速公路上行驶时发动机的功率为60kW,那么汽车行驶108 km,发动机做的功为多少? |
答案
| 解:(1)平均速度小,耗油量大 ; (2)m=  汽油V=0.8kg/L×8.5L=6.8kg 汽油V=0.8kg/L×8.5L=6.8kg (3)W=Pt=60×103×(108÷90)×3600 J=2.592×103J |
据专家权威分析,试题“节能是汽车性能的一个重要指标.但同一辆汽车每百公里的消耗与行驶..”主要考查你对 功的计算,密度公式的应用,物理常识 等考点的理解。关于这些考点的“档案”如下:
功的计算密度公式的应用物理常识
考点名称:功的计算
- 功的计算公式:
功(W)等于力(F)跟物体在力的方向上通过的距离(s)的乘积。(功=力×距离),W=FS。
单位:
国际单位制中,力的单位是N,距离的单位是m,功的单位是N·m,它有一个专用名称叫做焦耳,简称焦,用符号J表示,1J=1N·m。 - 在利用该公式进行计算时的注意点:
(1)力与物体移动的距离在方向上必须一致;
(2)力与物体移动的距离必须对应于同一物体;
(3)力与物体移动的距离必须对应于同一段时间。
考点名称:密度公式的应用
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比 。
。- 密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ = 总结规律后方可。
总结规律后方可。
如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为 ,ρ乙=
,ρ乙=  ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
2. 密度公式ρ = 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:
密度的公式是ρ = ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |


![如图所示的四个情景中,人对物体做功的是[]A.小军拉着重物静止不动B.小刚用力推汽车,汽车没动C.小丽用力搬起箱子D.小红背着书包在等车-九年级物理](http://www.00-edu.com/d/file/ks/wuli/1/135/2020-05-31/e5d802adaf13db272d6d88be41cd2cc8.gif)