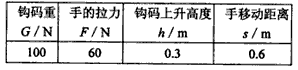
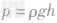如图所示,沿斜面把一个重50N的物体拉上去,所用拉力F=40N,斜面长5m,高3m,物体向上运动的速度为0.1m/s,求:(1)拉力F所做的有用功;(2)拉力F的功率;(3)斜面的机械效率;-八年级物理
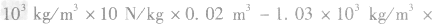
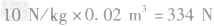
(3)由题图可知,海水阻力与机器人的运动速度成正比,当机器人运动速度为0.5m/s时,f=175N 机器人匀速前进时,机器人水平推进力F=f
P=Fv=175N×0.5m/s=87.5W
答案:(1)7.21×105Pa(2)334N(3)87.5W
考点名称:有用功和额外功
- 有用功,额外功与总功:
名称 定义 符号 公式 实例 有用功 使用机械做功时对人们有用的功 W有 W有=Gh 从井中打水时提水所做的功 额外功 对人们没有用但又不得不做的功 W额 —— 从井中打水时提水桶和绳子所做的功 总功 有用功与额外功之和 W总 W总=W有+W额 从井中打水时手的拉力所做的功 - 区分有用功和额外功:
区分有用功与额外功的关键是看我们需要达到什么做功目的。在同一做功过程中,目的不同,功的性质就不一样。例如:用桶将水从水井中提出来,提水是我们需要的,而提桶是不需要,但又不得不做的功,故克服水重做的是有用功,而克服桶重做的是额外功;如果是一只桶掉入水井里,我们要将桶从井中提出来,则克服桶重做的是有用功,而克服桶中可能带出来的水的重力所做的功就是额外功了。 计算有用功,额外功和总功的方法:
1. 总功的计算:
(1)定义法:W总=Fs
(2)总功等于有用功和额外功之和,即W总=W有用+W额外
(3)公式法:
2. 有用功的计算方法:
(1)定义法:W有用=Gh
(2)W有用=W总-W额外
(3)公式法:
3. 额外功的计算方法:
(1)定义法:
(2)W额外=W总-W有用
(3)公式法:
考点名称:斜面的机械效率
- 斜面的机械效率:
有用功 W有用=Gh 总功 W总=Fl
W总=Gh+fl
(f为摩擦力)额外功 W额外=W总-W有用
W额外=fl机械效率 
- 测量斜面的机械效率:
【实验目的】:测量斜面的机械效率
【器材】斜面,铁架台,小车,弹簧秤,米尺
【操作】
(1)照图那样安装好斜面,将小车放在斜面上。用弹簧秤缓慢地把小车拉上斜面,记下弹簧秤的示数F,测出小车沿斜面通过的距离L,用弹簧秤称得小车重G,并测出小车上升的高度h,算出斜面的效率η1=Gh/FL。
(2)把小车翻过来(轮子朝上)放在斜面上,重复上述实验,根据实验数据算出此时斜面效率η2。
(3)增大斜面的倾角,小车仍翻着放在斜面上重复实验,算出斜面效率η3。
比较η1、η2、η3的大小,可知η1>η2,η2<η3。分析实验结果可得:斜面的效率主要受斜面和小车间的摩擦的影响,在(1)中由于轮子和斜面间的滚动摩擦小,必需做的额外功少,效率就高。在(3)中,当倾角增大,车对斜面的压力减小,从而摩擦也减小,因此效率比(2)时高。比较操作(2)、(3)中的F及η的大小,可知斜面越省力其效率不一定越高。 - 提高斜面机械效率的方法:
在其他条件一定时,斜面的倾斜程度越大,机械效率越高,斜面表面粗糙程度越大,机械效率越低;机械效率与物体重量无关,物体斜面之间接触面大小无关。
例:如图所示,斜面高为1m,长为3m,工人用 400N沿斜面方向的力将重为840N的箱子拉到汽车上,在这过程中拉力做了______J的功,机械效率为______。要提高该斜面的机械效铝,应该_______。(写出一条措施)
解析: ,
,
提高机械效率的方法是减小总功,以增大有用功在总功中所占的比例。
答案:1200 70% 减小斜面的粗糙度
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:用图所示的滑轮组提升重物,已知物体重为200N,人用125N的拉力向下拉动绳子,5s内可使物体匀速上升2m求:(1)拉力所做的功和拉力的功率;(2)滑轮组的机械效率.-九年级物理
下一篇:如图所示,把同一物体分别沿AB、AC、AD三个斜面匀速推到同一高度的A点,不计摩擦力,则[]A.沿AB斜面最省力,做功最少B.沿AD斜面最省力,但做功最多C.沿三个斜面的推力一样大-八年级物理
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |


![如图所示的四个情景中,人对物体做功的是[]A.小军拉着重物静止不动B.小刚用力推汽车,汽车没动C.小丽用力搬起箱子D.小红背着书包在等车-九年级物理](http://www.00-edu.com/d/file/ks/wuli/1/135/2020-05-31/e5d802adaf13db272d6d88be41cd2cc8.gif)