如图是小明“探究斜面的机械效率与倾斜程度关系”的实验装置,他在实验时用弹簧测力计拉着重为6N的木块分别沿倾斜程度不同的同一斜面匀速向上运动,实验数据记录如下表。(1)在-九年级物理
题文
| 如图是小明“探究斜面的机械效率与倾斜程度关系”的实验装置,他在实验时用弹簧测力计拉着重为6N的木块分别沿倾斜程度不同的同一斜面匀速向上运动,实验数据记录如下表。 |
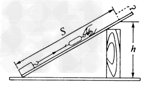 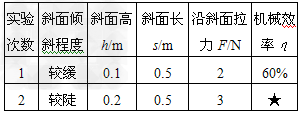 |
| (1)在第2次实验中拉力所做的额外功是 J,机械效率是 。 (2)小明完成两次实验后,得出的结论是:光滑程度一样的斜 面,其倾斜程度越大,机械效率越高。你觉得他的结论 (选填“可靠”或“不可靠”),理由是 。 (3)斜面 在生产、生活中随处可见。在盘山公路、镊子、螺丝钉、汽车方向盘中,应用了斜面的是 、 。 |
答案
| (1)0.3;80% ; (2)不可靠;实验次数太少,结论不具有普遍性;(第二空答案不唯一,只要能说出“实验次数太少”或“结论具有偶然性”等意思的答案都得分) (3)盘山公路;螺丝钉( 这两空的答案顺序可以颠倒) 。 |
据专家权威分析,试题“如图是小明“探究斜面的机械效率与倾斜程度关系”的实验装置,他在..”主要考查你对 功的计算公式的应用,有用功和额外功,斜面的机械效率,其他简单机械:轮轴和斜面 等考点的理解。关于这些考点的“档案”如下:
功的计算公式的应用有用功和额外功斜面的机械效率其他简单机械:轮轴和斜面
考点名称:功的计算公式的应用
- 应用:
利用功的计算公式加计算:F或S,F=W/s,s=W/F。 - 转换思想求功的大小 :
“转换思想方法”求功的大小。公式W=Fs中的s 必须是在力的方向通过的距离,而且F的大小一直保持不变,能运用功的公式求解,当作用在物体上的力的大小总在发生改变,则在求解功的时候注意不能直接利用公式W=Fs,应转换思想。如:平放在地上的一根均匀木料,现用一总垂直木料方向的力将它抬到竖直为止,则至少要做多少功?由于抬木料的力的大小、方向总在发生改变,而且木料通过的距离也不完全在力的方向上,故无法直接应用公式求解。我们根据功的原理可知:使用任何机械都不省功,则对物体所做的功等效于将物体重心提高所做的功,即可求解。
例:小明同学用一个距离手3m高的定滑轮拉住重100N的物体,从滑轮正下方沿水平方向移动4m如图所示,若不计绳重和摩擦,他至少做功( )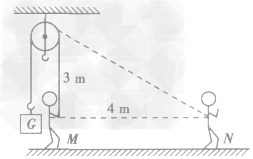
A.200JB.300J C.400JD.500J
解析:本题中由于不计绳重和摩擦,属于理想机械,可使用功的原理进行求解。人站在M处时,绳长3m,当人走到N处时,此时的绳长由勾股定理可知为5m,也就是说人从M点走到N点拉下的长度为2m,即物体上升的高度h=2m。小明对绳做功至少是克服物重G所做的功,即W=Gh=100N×2m=200J。
答案:A
考点名称:有用功和额外功
- 有用功,额外功与总功:
名称 定义 符号 公式 实例 有用功 使用机械做功时对人们有用的功 W有 W有=Gh 从井中打水时提水所做的功 额外功 对人们没有用但又不得不做的功 W额 —— 从井中打水时提水桶和绳子所做的功 总功 有用功与额外功之和 W总 W总=W有+W额 从井中打水时手的拉力所做的功 - 区分有用功和额外功:
区分有用功与额外功的关键是看我们需要达到什么做功目的。在同一做功过程中,目的不同,功的性质就不一样。例如:用桶将水从水井中提出来,提水是我们需要的,而提桶是不需要,但又不得不做的功,故克服水重做的是有用功,而克服桶重做的是额外功;如果是一只桶掉入水井里,我们要将桶从井中提出来,则克服桶重做的是有用功,而克服桶中可能带出来的水的重力所做的功就是额外功了。 计算有用功,额外功和总功的方法:
1. 总功的计算:
(1)定义法:W总=Fs
(2)总功等于有用功和额外功之和,即W总=W有用+W额外
(3)公式法:
2. 有用功的计算方法:
(1)定义法:W有用=Gh
(2)W有用=W总-W额外
(3)公式法: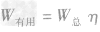
3. 额外功的计算方法:
(1)定义法:
(2)W额外=W总-W有用
(3)公式法: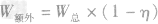
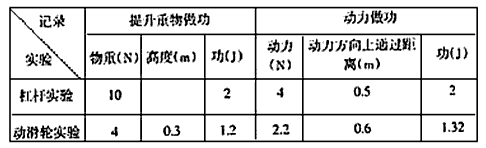
考点名称:斜面的机械效率
- 斜面的机械效率:



![用大小不同的甲、乙两个力拉同一物体,两力所做的功W与在这两个力的方向上移动的距离S的关系图象如图,由图可知,甲、乙两个力的大小关系是[]A.F甲>F乙B.F甲<F乙C.F甲=F乙D.-九年级物理](http://www.00-edu.com/d/file/ks/wuli/1/136/2020-06-01/dea013ab270bb8f078766792740fec88.png)
