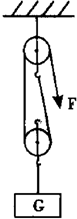
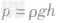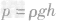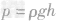如图所示,工人在10s内用滑轮组将质量为l0kg的箱子匀速竖直升了2m,此时的机械效率为80%(不计绳重和摩擦,取g=10N/kg).求:(l)工人做的有用功;(2)工人施加的拉力;(3)工人所-物理
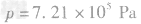
(2)物体在水下受平衡力的作用,则
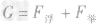
则

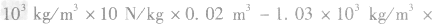
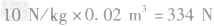
(3)由题图可知,海水阻力与机器人的运动速度成正比,当机器人运动速度为0.5m/s时,f=175N 机器人匀速前进时,机器人水平推进力F=f
P=Fv=175N×0.5m/s=87.5W
答案:(1)7.21×105Pa(2)334N(3)87.5W
考点名称:有用功和额外功
- 有用功,额外功与总功:
名称 定义 符号 公式 实例 有用功 使用机械做功时对人们有用的功 W有 W有=Gh 从井中打水时提水所做的功 额外功 对人们没有用但又不得不做的功 W额 —— 从井中打水时提水桶和绳子所做的功 总功 有用功与额外功之和 W总 W总=W有+W额 从井中打水时手的拉力所做的功 - 区分有用功和额外功:
区分有用功与额外功的关键是看我们需要达到什么做功目的。在同一做功过程中,目的不同,功的性质就不一样。例如:用桶将水从水井中提出来,提水是我们需要的,而提桶是不需要,但又不得不做的功,故克服水重做的是有用功,而克服桶重做的是额外功;如果是一只桶掉入水井里,我们要将桶从井中提出来,则克服桶重做的是有用功,而克服桶中可能带出来的水的重力所做的功就是额外功了。 计算有用功,额外功和总功的方法:
1. 总功的计算:
(1)定义法:W总=Fs
(2)总功等于有用功和额外功之和,即W总=W有用+W额外
(3)公式法:
2. 有用功的计算方法:
(1)定义法:W有用=Gh
(2)W有用=W总-W额外
(3)公式法:
3. 额外功的计算方法:
(1)定义法:
(2)W额外=W总-W有用
(3)公式法:
考点名称:滑轮(组)中拉力的计算
- 滑轮组的省力情况:
使用滑轮组时,滑轮组由几段绳子吊着动滑轮,提起物体所用的力就是物重的几分之一。 - 滑轮组由几股绳子承担物重:
有几股绳与动滑轮相连,承担物重的绳子的股数n 就是几,而重物上升的高度h与绳子自由端移动的距离s的关系是:s=nh。如图:在动、定滑轮之间画一条线,将它们分开,只算在动滑轮上的绳子的股数。
例1如图甲、乙滑轮组装置,所有摩擦不计,分别用F1、F2竖直匀速拉动重物G,已知每个滑轮重力为 G/2,则力F1和F2之比为( )
A.1:1B.3:2C.2:3D.3:4
解析:当考虑动滑轮的重力,不计摩擦时,F= ,由图中滑轮组的绕线方法可知:F1=
,由图中滑轮组的绕线方法可知:F1=
 。
。
答案:C
滑轮组省力情况的判断
1.滑轮组竖放:若不考虑动滑轮自重以及绳、轮摩擦,滑轮组用几股绳子吊着物体,提起物体所用的动力就是物重的几分之一,即 ;若考虑动滑轮自重,但忽略摩擦,此式变为F拉=
;若考虑动滑轮自重,但忽略摩擦,此式变为F拉=  。用“连动法”,弄清直接与动滑轮连接的绳子的根数n,在图甲中我们以重物和动滑轮为研究对象,n=4,有四根绳子承担动滑轮及重物,所以用力
。用“连动法”,弄清直接与动滑轮连接的绳子的根数n,在图甲中我们以重物和动滑轮为研究对象,n=4,有四根绳子承担动滑轮及重物,所以用力 。同理,分析乙图可知,提起重物及动滑轮的
。同理,分析乙图可知,提起重物及动滑轮的 。
。
2.滑轮组横放:在不考虑绳、轮摩擦时,滑轮组用几股绳拉着物体做匀速直线运动,拉力大小就是物体所受摩擦力的几分之一,即: 。
。
例1同一物体沿相同的水平地面被匀速移动,如下图所示,托力分别为F甲、F乙、F丙,不记滑轮与轻绳间的摩擦,比较它们的大小,则( )
A.F甲<F乙<F丙
B.F甲>F乙>F丙
C.F甲>F乙=F丙
D.F甲=F乙>F丙
解析:三种情况下物体与地面的摩擦都相等为f,甲是定滑轮,F甲=f,乙是动滑轮, ,丙是滑轮组,
,丙是滑轮组, ,即
,即 ,选B。
,选B。
例2如图甲所示,物体4在拉力F的作用下做匀速直线运动,弹簧测力计的示数是5N,那么拉力,为_____N,物体A与地面间的摩擦力为_____N。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:两台机器做功之比为5﹕2,所用时间之比为2﹕5,则它们的功率之比为()A.1﹕1B.5﹕2C.4﹕25D.25﹕4-物理
下一篇:在平直的公路上以一般的速度行驶的自行车所受的阻力为车与人总重的0.02倍,则骑车人的功率最接近于()A.100WB.1WC.1KWD.10KW-物理
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |