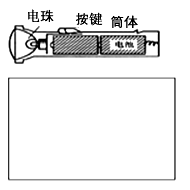
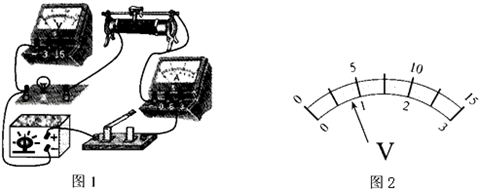
亲爱的同学:您会使用下面的基本实验仪器吗?(1)用同一支温度计分别

解得t1=20℃

解得t2=40℃

考点名称:电路图及元件符号
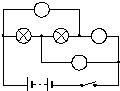
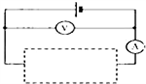
电路图:电路图主要由元件符号、连线、结点、注释四大部分组成,用规定的符号表示电路连接情况的图叫做电路图;
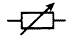
元件符号:表示实际电路中的元件,它的形状与实际的元件不一定相似,甚至完全不一样。但是它一般都表示出了元件的特点,而且引脚的数目都和实际元件保持一致。
几种常见的元件符号如下:

常见元器件作用:

电路图的功能及作用:
①电路图主要用来讲述电路的工作原理。
②它能够完整地表达某一级电路的结构和工作原理,有时还全部标出电路中各元器件的参数,如标称阻值、标称容量和三极管型号等。
③它对深入理解电路的工作原理和记忆电路的结构、组成很有帮助。
考点名称:电功或电能的计算
电能是表示电流做多少功的物理量,电能指电以各种形式做功的能力(所以有时也叫电功 ),分为直流电能、交流电能,这两种电能均可相互转换。
电功计算基本公式及推导公式(适用于纯电阻电路):W=UIt,W=I2Rt,W=U2t/R,W=Pt,W=Uq。
电能单位是“度”,它的学名叫做千瓦时,符号是kW·h。在物理学中,更常用的能量单位(也就是主单位,有时也叫国际单位)是焦耳,简称焦,符号是J。它们的关系是:1kW·h=3.6×106J,电能公式:W=UIt=Pt 根据欧姆定律(I=U/R)可以进一步推出:W=I2Rt=U2t/R
电功计算:
1. W=UQ电
电能也是一种能量,而这种能量的实施者就是电荷,电荷量就是这种能量在一般的时间内所有参与作功从A点到B点的实行者,每个电荷从A点到B点做的功就是电压,两者相乘就是AB的电功,就是消耗的电能
2. W=UIt
我们来看一下电功的含义,电功通俗的讲就是AB之间的一段时间A点到B点所消耗的电能(A点到B点可以是一个用电器,也可以是一部分电路)电压的实质是一个单位的电荷从A点到B点所做的功,电流提供的是在一个单位时间内AB之间的电荷量,时间也有了,那么AB之间的电荷量在一定时间内从A点到B点所做的功也就是消耗的电能就是W=UIt
3. W=Pt
W电功、P电功率、t时间
像功的计算方法一样就是功率乘以时间,在生活中可以理解为工作总量=工作效率×工作时间,同样道理电所做的功当就等于电做功的效率乘以时间。
W=I2Rt (纯电阻电路)
考点名称:长度的测量及刻度尺的使用
特殊的长度测量:
在测量长度的过程中,经常会遇到一些不好直接测量或由于物体形状特殊无法直接测量的问题,如细铜丝的直径、圆柱体的周长、硬币的直径、油筒内最长的直线、电线杆的高度等
测量方法汇总:
一、测多算少法
由于测量工具精确度的限制,某些微小量,无法直接测量,在测量时,可以把若干个相同的微小量,集中起来,做为一个整体进行测量,将测出的总量除以微小量的个数,就可以得出被测量的值,这种测量方法叫做“测多算少法”。
例如:用普通的毫米刻度尺测一张纸的厚度,我们可以先用刻度尺去测100张同样纸的厚度。然后用这个数值除以100,即得出一张纸的厚度。再如:测量细铜丝的直径,可以把细铜丝在铅笔上紧密排绕成线圈,用刻度尺测出线圈的长度,并数出圈数,然后用线圈的长度除以圈数,即得细铜丝的直径。
二、量小求大法
由于被测量物体的长度远远超过了刻度尺的最大测量值,不便于用刻度尺测量,可先选取一个小物体或一小部分,用刻度尺测取其长度,然后设法测出大物体与小物体(或小部分)的倍数关系,最后根据这一倍数关系求得大物体的长度,这种测量方法被称为“量小求大法”。
例如:测一大卷粗细均匀的细铜线的长度。由于细铜线长度数值非常大,远远超出了普通刻度尺的最大测量值,不便于直接测量。我们可以先截取一小段细铜线,用刻度尺测出其长度为L,然后用天平分别测出所有细铜线的质量和截取的小段细铜线质量,两者相除求得其倍数关系为n,则这一大卷细铜线的总长度为nL。又如:测量操场跑道的长度,普通刻度尺无能为力,可以用刻度尺设法测出自行车轮子的周长,然后骑自行车绕跑道一圈,数出轮子转过的圈数,用圈数乘以轮子的周长,即为操场跑道的长度。
三、变曲为直法
长度测量时,要求刻度尺应紧靠被测物体,在实际测量中,有些长度并非直线,如地图上铁路或河流的长度、圆柱体的周长等,无法直接测量,可以借助于易弯曲但弹性不大的细棉线等,与被测物体紧密接触,然后量出细棉线的长度即可,此种方法被称为“变曲为直法”。
例如:要测量地图上北京到上海铁路线的长度,我们可以找一根细棉线,使其与地图上北京到上海铁路线完全重叠,并在棉线的两端做上标记,拉直棉线,用刻度尺测出标记间距离即为地图上两地间的距离,借助于比例尺我们还可以求出两地间铁路线的实际长度。又如:测量圆柱体的周长,我们可以借助于纸带或细棉线,平行于圆柱体横截面紧紧围住圆柱体,在重叠处做标记,展开纸带或细棉线,用刻度尺测出标记间的距离,即为圆柱体的周长。
四、化暗为明法
有些物体的长度不是明显的暴露在外面,而是隐含在物体内部或凹部,无法用刻度尺测量,我们可以借助于其它工具或方法,使该长度显露出来,这种方法被称为“化暗为明法”。

例如:不借助于任何其它仪器,不经任何计算利用粉笔和长度足够的刻度尺,测出长方体内最长的直线距离。长方体内最长的直线距离为其斜对角线的长度,即图甲中AG、BA、CE、DF中的任意一条,但由于位于长方体内部,无法直接测量,具体办法是:用粉笔在地面上依EFGH顺序把下表面的长方形画出来,设其为E′F′G′H′,然后将长方体向右平移,使H′G′与EF重合,如图乙所示:此时的AF′或BE′即为长方体内量长的直线距离。已经显露在外,可以直接测量了。又如:测一小口容器的深度,可用一直杆竖直插入到容器的底部,在与容器口相平处做一标记,然后用刻度尺量出标记到杆端的距离即为该容器的深度。
五、卡测法
对于部分形状规则的物体,某些长度端点位置模糊,或不易确定,如圆柱体、乒乓球的直径,圆锥体的高等,需要借助于三角板或桌面将待测物体卡住,把不可直接测量的长度转移到刻度尺上,从而直接测出该长度,这种测量方法叫做“卡测法”。如:圆柱体直径测量方法如下图。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |