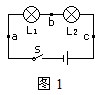
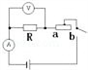
两根电热丝,其电阻R1=2R2.若将它们串联在电路中,保持电源电压不
(2)U=IR,当电流一定时,导体两端的电压跟它的电阻成正比。不能说成导体的电阻一定时导体两端的电压与通过的电流成正比,因为电压是形成电流的原因。电压的大小由电源决定,跟I、R无关,此式在计算比值时成立,不存在任何物理意义。
(3)R=U/I,此公式也是一个量变式,不存在任何物理意义。不能误认为导体的电阻跟导体两端的电压成正比,跟导体中的电流成反比。公式中的I、U、R都要用国际单位,即电流的单位为安培,符号A;电压的单位为伏特,符号V;电阻的单位为欧姆,符号Ω。
3.要明白定律的适用范围
(1)定律只适用于金属导电和液体导电,对于气体、半导体导电一般不适用。
(2)定律只适用于纯电阻电路。如:电路中只接有电阻器、电热器、白炽灯等用电器的电路。对于非纯电阻电路,如:电动机电路、日光灯电路等,则不能直接应用。
4.要理解欧姆定律的注意事项
(1)物理量的同一性。叙述欧姆定律时,在两个 “跟”字后面都强调了“这段导体”四个字,它是指对电路中同一导体或同一电路而言。所以在运用欧姆定律I=U/R等进行计算时,必须注意同一性,即I、R、U必须是 同一导体或同一段电路中的物理量。在表示I、U、R 时,注意脚标的一一对应。
(2)物理量的同时性。由于电路的连接方式发生改变,开关的断开或闭合,或滑动变阻器滑片的左右移动都可能使电路中总电阻发生变化,从而可能引起电路中电流和各部分电阻两端的电压发生变化。因此,必须注意在同一时刻、同一过程中的电压、电阻与电流的相互对应,不可将前后过程的I、R、U随意混用。
欧姆定律知识框架:

欧姆定律解题技巧
根据串、并联电路的特点和欧姆定律的公式可进行有关计算。
解题的方法是:
(1)根据题意画出电路图,看清电路的组成(串联还是并联);
(2)明确题目给出的已知条件与未知条件,并在电路图上标明;
(3)针对电路特点依据欧姆定律进行分析;
(4)列式解答。
考点名称:串联电路的电流规律
串联电路特点:
串联电路中,电流处处相等,即I=I1=I2=…=In。在串联电路中只要测出任何一个位置的电流,就知道了其他位置的电流。
实验探究串联电路的电流规律:
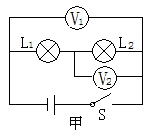
1. 实验电路:

2. 实验步骤:
(1)根据串联电路的电路图,组装好实验装置
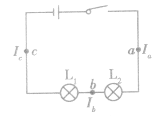
(2)选用电流表的最大量程,并把电流表接在电路的a处。
(3)合上开关,测出a处的电流值。
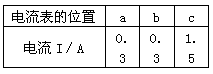
(4)把电流表先后改接在电路中的b、c处,分别测出电流值,并对电路中Ia、Ib、Ic进行比较分析。
3. 结论:串联电路各处电流都相等Ia=Ib=Ic。
考点名称:焦耳定律及计算公式
焦耳的定律及公式:
焦耳定律或焦耳-冷次定律是定量说明传导电流将电能转换为热能的定律。1841年,英国物理学家詹姆斯·焦耳发现载流导体中产生的热量Q(称为焦耳热)与电流I的平方、导体的电阻R和通电时间t成比例。而在1842年时,俄国物理学家海因里希·楞次也独立发现上述的关系,因此也称为“焦耳-冷次定律”。
采用国际单位制时,焦耳定律的表达式为:
Q = I2Rt 或 P = I2R
其中Q(热量)、I(电流)、R(电阻)、t(时间)、P(热功率)各量的单位依次为焦耳、安培、欧姆、秒和瓦特。
焦耳定律是设计电照明,电热设备及计算各种电气设备温升的重要公式。
与欧姆定律的关系:
根据欧姆定律:
U=IR
焦耳定律的公式亦可表示为:

关于焦耳定律的历史:
关于导体中通过的电流与所产生的热量之间的定律。1840年由詹姆斯·普雷斯科特·焦耳提出。定律揭示了电流通过导线时所产生的热量和导线的电阻与电流平方的乘积成比例,即
H=0.24IRt
式中H 为产生的总热量,单位为卡;I 为电流,单位为安;R 为电阻,单位为欧;t为时间,单位为秒;0.24为由实验定出的比例常量。
焦耳是通过实验测定发现这个定律的。但是从理论上也不难理解,当电流的大小不变,产生的热量全部来源于电荷通过导体失去的势能。电荷的数量为It,失去的势能为W,W=RIt。因此,在单位时间中转变为热的电能为RI(焦),或者说在导体上消耗的电功率P为
P=RI(瓦)
焦耳定律是设计电照明,电热设备及计算各种电气设备温升的重要公式。
焦耳定律在串联电路中的运用:
在串联电路中,电流是相等的,则电阻越大时,产生的热越多。
焦耳定律在并联电路中的运用:
在并联电路中,电压是相等的,通过变形公式,W=Q=Pt=(U^2/R)×t,当U定时,R越大则Q越小。
需要注明的是,焦耳定律与电功公式W=UIt适任何元件及发热的计算,即只有在像电热器这样的电路(纯电阻电路)中才可用Q=W=UItq=I^2×Rt =(U^2/R)×t。
另外,焦耳定律还可变形为Q=IRq(后面的Q是电荷量,单位库仑(c))。
在热力学中指,气体的内能只是温度的函数,与体积无关。即内能对体积的偏导数为零。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |